题目内容
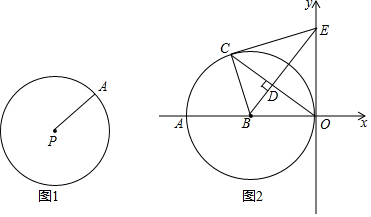
3.【圆的概念】在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆,如图1所示,换言之,到某个定点等于定长的所有点在同一个圆上.【拓展延伸】圆心在P(a,b),半径为r的圆的方程可写为:(x-a)2+(y-b)2=r2.
例如:圆心在P(-1,-2),半径为5的圆的方程可写为:(x-2)2+(y+1)2=25.
(1)请填空:
①以A(3,0)为圆心,半径为1的圆的方程为:(x-3)2+y2=1;
②以B(-1,-2)为圆心,半径为$\sqrt{3}$的圆的方程为:(x+1)2+(y+2)2=3;
(2)请根据以上材料解决下列问题:
如图2所示,以B(-6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC,垂足为D,延长BD交y轴于点E,已知∠AOC=$\frac{3}{5}$.
①连接EC,判断EC和⊙B的位置关系,并说明理由;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求出P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程,若不存在,说明理由.
分析 (1)根据阅读材料中的定义求解;
(2)①根据垂径定理由BD⊥OC得到CD=OD,则BE垂直平分OC,再根据线段垂直平分线的性质得EO=EC,则∠EOC=∠ECO,加上∠BOC=∠BCO,易得∠BOE=∠BCE=90°,然后根据切线的判定定理得到EC是⊙B的切线;
②由∠BOE=∠BCE=90°,根据圆周角定理得点C和点O偶在以BE为直径的圆上,即当P点为BE的中点时,满足PB=PC=PE=PO,利用同角的余角相等得∠BOE=∠AOC,则sin∠BOE=sin∠AOC=$\frac{3}{5}$,在Rt△BOE中,利用正弦的定义计算出BE=10,利用勾股定理计算出OE=8,则E点坐标为(0,8),于是得到线段AB的中点P的坐标为(-3,4),PB=5,然后写出以P(-3,4)为圆心,以5为半径的⊙P的方程.
解答 (1)解:①以A(3,0)为圆心,1为半径的圆的方程为(x-3)2+y2=1;
②以B(-1,-2)为圆心,$\sqrt{3}$为半径的圆的方程为(x+1)2+(y+2)2=3;
故答案为(x-3)2+y2=1;(x+1)2+(y+2)2=3; (2)①证明:∵BD⊥OC,
(2)①证明:∵BD⊥OC,
∴CD=OD,
∴BE垂直平分OC,
∴EO=EC,
∴∠EOC=∠ECO,
∵BO=BC,
∴∠BOC=∠BCO,
∴∠EOC+∠BOC=∠ECO+∠BCO,
∴∠BOE=∠BCE=90°,
∴BC⊥CE,
∴EC是⊙B的切线;
②存在.
∵∠BOE=∠BCE=90°,
∴点C和点O偶在以BE为直径的圆上,
∴当P点为BE的中点时,满足PB=PC=PE=PO,
∵B点坐标为(-6,0),
∴OB=6,
∵∠AOC+∠DOE=90°,∠DOE+∠BEO=90°,
∴∠BEO=∠AOC,
∴sin∠BEO=sin∠AOC=$\frac{3}{5}$,
在Rt△BOE中,sin∠BEO=$\frac{OB}{BE}$,
∴$\frac{6}{BE}$=$\frac{3}{5}$,
∴BE=10,
∴OE=$\sqrt{B{E}^{2}-O{B}^{2}}$=8,
∴E点坐标为(0,8),
∴线段AB的中点P的坐标为(-3,4),PB=5,
∴以P(-3,4)为圆心,以5为半径的⊙P的方程为(x+3)2+(y-4)2=25.
点评 本题了圆的综合题:熟练掌握垂径定理、切线的判定定理、圆周角定理和等腰三角形的性质;阅读理解能力也是本题考查的重点;会运用锐角三角函数的定义和勾股定理进行几何计算.

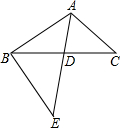 如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )| A. | $\frac{20}{3}$ | B. | $\frac{17}{4}$ | C. | $\frac{16}{3}$ | D. | $\frac{15}{4}$ |