题目内容
10．
如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．步骤1：以C为圆心，CA为半径画弧①；
步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；
步骤3：连接AD，交BC延长线于点H．
下列叙述正确的是（ ）
| A． | BH垂直平分线段AD | B． | AC平分∠BAD | ||
| C． | S△ABC=BC•AH | D． | AB=AD |
分析 根据已知条件可知直线BC是线段AD的垂直平分线，由此一一判定即可．
解答 解：A、正确．
如图连接CD、BD，
∵CA=CD，BA=BD，
∴点C、点B在线段AD的垂直平分线上，
∴直线BC是线段AD的垂直平分线，
故A正确．
B、错误．CA不一定平分∠BDA．
C、错误．应该是S△ABC=$\frac{1}{2}$•BC•AH．
D、错误．根据条件AB不一定等于AD．
故选A．
点评 本题考查作图-基本作图、线段的垂直平分线的性质等知识，解题的关键是掌握证明线段垂直平分线的证明方法，属于基础题，中考常考题型．
练习册系列答案
阅读快车系列答案
相关题目
1．有一正角锥的底面为正三角形．若此正角锥其中两个面的周长分别为27、15，则此正角锥所有边的长度和为多少？（ ）
| A． | 36 | B． | 42 | C． | 45 | D． | 48 |
在平面直角坐标系中，直线l：y=x-1与x轴交于点A1，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点Bn的坐标是（2n-1，2n-1）．
15．
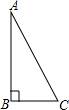在一次数学课上，张老师布置了一项作业：以Rt△ABC（如图所示）的两直角边AB，BC为邻边作矩形ABCD，下面是小钟和小国各自的作法：
小孟说：“他们的作法都错误．”你的观点是（ ）
在一次数学课上，张老师布置了一项作业：以Rt△ABC（如图所示）的两直角边AB，BC为邻边作矩形ABCD，下面是小钟和小国各自的作法：| 小钟作法： （1）作AC的垂直平分线MN，垂足为点O； （2）连接BO，并延长BO至点D，使DO=BO； （3）连接AD，CD 所以，四边形ABCD就是所要求作的矩形 |
| 小国作法： （1）分别以A，C为圆心，以BC，AB为半径作弧，两弧交于点D； （2）连接AD，CD． 所以，四边形ABCD就是所要求作的矩形． |
| A． | 小钟的作法正确 | B． | 小国的作法正确 | ||
| C． | 小钟和小国的作法都正确 | D． | 赞同小孟的观点 |
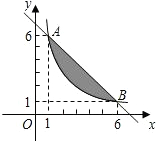如图，A、B两点在函数y=$\frac{y}{x}$（x＞0）的图象上．