题目内容
2.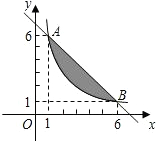 如图,A、B两点在函数y=$\frac{y}{x}$(x>0)的图象上.
如图,A、B两点在函数y=$\frac{y}{x}$(x>0)的图象上.(1)求k的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.若点(m,n)是第一象限内位于直线AB的图象下方的格点,求这个点在图中阴影部分(不包括边界)内部的概率.
分析 (1)将A点或B点的坐标代入y=$\frac{k}{x}$求出k,再将这两点的坐标代入y=mx+n求出m、n的值即可得到这个函数的解析式;
(2)画出网格图帮助解答.
解答 解:(1)由图象可知,函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,6),
可得k=6.
设直线AB的解析式为y=mx+n.
∵A(1,6),B(6,1)两点在函数y=mx+n的图象上,
∴$\left\{\begin{array}{l}{m+n=6}\\{6m+n=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-1}\\{n=7}\end{array}\right.$.
∴直线AB的解析式为y=-x+7;
(2)图中在直线AB的图象下方的格点是(1,1),(2,1),(3,1),(4,1),(5,1),(1,2),(2,2),(3,2),(4,2),(1,3),(2,3),(3,3),(1,4),(2,4),(1,5),
阴影部分(不包括边界)所含格点是(2,4),(3,3),(4,2)共3个,
∴P=$\frac{3}{15}$=$\frac{1}{5}$.
点评 本题考查了一次函数和反比例函数的图象性质,待定系数法求一次函数的解析式以及几何概率,综合性较强,体现了数形结合的思想.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
10. 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
| A. | BH垂直平分线段AD | B. | AC平分∠BAD | ||
| C. | S△ABC=BC•AH | D. | AB=AD |
17.“一方有难,八方支援”,雅安芦山4•20地震后,某单位为一中学捐赠了一批新桌椅,学校组织初一年级200名学生搬桌椅.规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)的套数为( )
| A. | 60 | B. | 70 | C. | 80 | D. | 90 |
14. 在1-7月份,某种水果的每斤进价与售价的信息如图所示,则出售该种水果每斤利润最大的月份是( )
在1-7月份,某种水果的每斤进价与售价的信息如图所示,则出售该种水果每斤利润最大的月份是( )
 在1-7月份,某种水果的每斤进价与售价的信息如图所示,则出售该种水果每斤利润最大的月份是( )
在1-7月份,某种水果的每斤进价与售价的信息如图所示,则出售该种水果每斤利润最大的月份是( )| A. | 3月份 | B. | 4月份 | C. | 5月份 | D. | 6月份 |
11. 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
其中,m=0.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有3个交点,所以对应的方程x2-2|x|=0有3个实数根;
②方程x2-2|x|=2有2个实数根;
③关于x的方程x2-2|x|=a有4个实数根时,a的取值范围是-1<a<0.
 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | 3 | $\frac{5}{4}$ | m | -1 | 0 | -1 | 0 | $\frac{5}{4}$ | 3 | … |
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有3个交点,所以对应的方程x2-2|x|=0有3个实数根;
②方程x2-2|x|=2有2个实数根;
③关于x的方程x2-2|x|=a有4个实数根时,a的取值范围是-1<a<0.
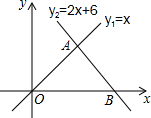 如图,直线l1:y1=x和直线l2:y2=-2x+6相交于点A,直线l2与x轴交于点B,动点P沿路线O→A→B运动.
如图,直线l1:y1=x和直线l2:y2=-2x+6相交于点A,直线l2与x轴交于点B,动点P沿路线O→A→B运动.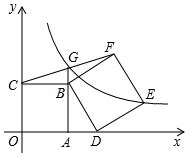 如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.
如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.