题目内容
15.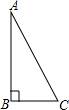 在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:
在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:| 小钟作法: (1)作AC的垂直平分线MN,垂足为点O; (2)连接BO,并延长BO至点D,使DO=BO; (3)连接AD,CD 所以,四边形ABCD就是所要求作的矩形 |
| 小国作法: (1)分别以A,C为圆心,以BC,AB为半径作弧,两弧交于点D; (2)连接AD,CD. 所以,四边形ABCD就是所要求作的矩形. |
| A. | 小钟的作法正确 | B. | 小国的作法正确 | ||
| C. | 小钟和小国的作法都正确 | D. | 赞同小孟的观点 |
分析 根据矩形的判定方法一一判断即可.
解答 解:根据小钟的作法 可知,OA=OC,OB=OD,
可知,OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,OA=OC,
∴OB=OA=OC=OD,
∴AC=BD,
∴四边形ABCD是矩形.
∴小钟的作法正确.
根据小国的作法,可知:AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形.
∴小国的作法正确.
故选C.
点评 本题考查矩形的判定、基本作图等知识,解题的关键是熟练掌握矩形判定方法,记住对角线相等的平行四边形是矩形,有一个角是90度的平行四边形是直角,属于中考常考题型.

练习册系列答案
相关题目
10. 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
| A. | BH垂直平分线段AD | B. | AC平分∠BAD | ||
| C. | S△ABC=BC•AH | D. | AB=AD |
4.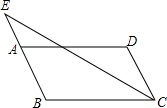 如图,在?ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )
如图,在?ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )
 如图,在?ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )
如图,在?ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )| A. | 3 | B. | 2.5 | C. | 2 | D. | 1.5 |
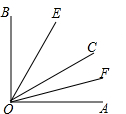 如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC. 如图,直线AB解析式为y=2x+4,C(0,-4),AB交x轴于A,A为抛物线顶点,交y轴于C,
如图,直线AB解析式为y=2x+4,C(0,-4),AB交x轴于A,A为抛物线顶点,交y轴于C,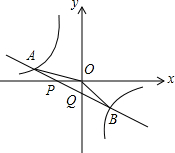 如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,其中正确的结论的序号是②③④.
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,其中正确的结论的序号是②③④.