题目内容
7.已知抛物线y=a(x-1)2-3(a≠0)的图象与y轴交于点A(0,-2),顶点为B.(1)试确定a的值,并写出B点的坐标;
(2)若一次函数的图象经过A、B两点,试写出一次函数的解析式;
(3)试在x轴上求一点P,使得△PAB的周长取最小值;
(4)若将抛物线平移m(m≠0)个单位,所得新抛物线的顶点记作C,与原抛物线的交点记作D,问:点O、C、D能否在同一条直线上?若能,请求出m的值;若不能,请说明理由.

分析 (1)把A(0,-2)代入y=a(x-1)2-3即可得到结论;
(2)设一次函数的解析式为y=kx+b将A、B两点的坐标代入解析式解方程组即可得到结论;
(3)连接EB交x轴于点P,则P点即为所求,求出过E、B点的一次函数解析式为y=-5x+2,即可得到结论;
(4)如图2,设抛物线向右平移m(若m>0表示向右平移,若m<0表示向左平移)个单位,得到新的抛物线的顶点C(1+m,-3),解方程组得到两抛物线的交点D($1+\frac{m}{2},\frac{m^2}{4}-3$),解一元二次方程得到m=2或m=-3,即可得到结论.
解答  解:(1)把A(0,-2)代入y=a(x-1)2-3得-2=a(0-1)2-3,解得:a=1,
解:(1)把A(0,-2)代入y=a(x-1)2-3得-2=a(0-1)2-3,解得:a=1,
∵顶点为B,
∴B(1,-3);
(2)设一次函数的解析式为y=kx+b
将A、B两点的坐标代入解析式求得:$\left\{\begin{array}{l}{-2=b}\\{-3=k+b}\end{array}\right.$,
∴k=-1,b=-2,
∴写出一次函数的解析式为y=-x-2,;
(3)A点关于x轴的对称点记作E,则E(0,2),
如图1,连接EB交x轴于点P,则P点即为所求,
理由:在△PAB中,AB为定值,
只需PA+PB取最小值即可,
而PA=PE,从而只需PE+PB取最小值即可,
∵两点之间线段最短,
∴PE+PB≤EB,
∴E、P、B三点在同一条直线上时,取得最小值.
由于过E、B点的一次函数解析式为y=-5x+2,
当y=0时,x=$\frac{2}{5}$,
∴P($\frac{2}{5}$,0);
(4)如图2,设抛物线向右平移m(若m>0表示向右平移,若m<0表示向左平移)个单位,
则所得新的抛物线的顶点C(1+m,-3),
∴新抛物线解析式为 y=(x-1-m)2-3
解$\left\{\begin{array}{l}{y=(x-1-m)^{2}-3}\\{y=(x-1)^{2}-3}\end{array}\right.$得$\left\{\begin{array}{l}{x=1+\frac{m}{2}}\\{y=\frac{{m}^{2}}{4}-3}\end{array}\right.$,
∴两抛物线的交点D($1+\frac{m}{2},\frac{m^2}{4}-3$),
∴经过O、C的一次函数解析式是y=-$\frac{3}{1+m}$x,若 O、C、D在同一直线上,
则 有$\frac{m^2}{4}-3=-\frac{3}{1+m}(1+\frac{m}{2})$,
化简整理得m3+m2-6m=0,
∵m≠0,
∴m2+m-6=0,解得:m=2或m=-3,
∴O、C、D三点能够在同一直线上,
此时m=2或m=-3.
即抛物线向右平移2个单位,或者向左平移3个单位,均满足题目要求.
点评 本题考查了待定系数法求函数的解析式,二次函数的性质,平移的性质,解一元二次方程,轴对称-最短距离问题,熟练掌握二次函数的性质是解题的关键.

| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{1}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
| A. | BH垂直平分线段AD | B. | AC平分∠BAD | ||
| C. | S△ABC=BC•AH | D. | AB=AD |
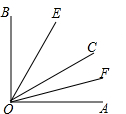 如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.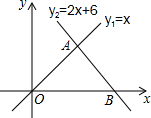 如图,直线l1:y1=x和直线l2:y2=-2x+6相交于点A,直线l2与x轴交于点B,动点P沿路线O→A→B运动.
如图,直线l1:y1=x和直线l2:y2=-2x+6相交于点A,直线l2与x轴交于点B,动点P沿路线O→A→B运动.