题目内容
19．如图1，在矩形ABCD中，动点P从点B出发，以每秒2个单位长度，沿BC-CD-DA运动至点A停止，设点P运动的时间为x秒，△ABP的面积为y．如果y关于x的变化情况如图2所示，则△ABC的面积是（ ）
| A． | 10 | B． | 20 | C． | 40 | D． | 80 |
分析 本题难点在于应找到面积不变的开始与结束，得到BC，CD的具体值．
解答 解：动点P从点B出发，沿BC、CD、DA运动至点A停止，而当点P运动到点C，D之间时，△ABP的面积不变．函数图象上横轴表示点P运动的路程，x=4时，y开始不变，说明BC=8，x=9时，接着变化，说明CD=2（9-4）=10．
∴△ABC的面积为=$\frac{1}{2}$×8×10=40．
故选C．
点评 本题考查了动点问题的函数图象，解决本题应首先看清横轴和纵轴表示的量．
练习册系列答案
名校课堂系列答案
相关题目
10．
如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．
步骤1：以C为圆心，CA为半径画弧①；
步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；
步骤3：连接AD，交BC延长线于点H．
下列叙述正确的是（ ）
如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．步骤1：以C为圆心，CA为半径画弧①；
步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；
步骤3：连接AD，交BC延长线于点H．
下列叙述正确的是（ ）
| A． | BH垂直平分线段AD | B． | AC平分∠BAD | ||
| C． | S△ABC=BC•AH | D． | AB=AD |
14．
在1-7月份，某种水果的每斤进价与售价的信息如图所示，则出售该种水果每斤利润最大的月份是（ ）
在1-7月份，某种水果的每斤进价与售价的信息如图所示，则出售该种水果每斤利润最大的月份是（ ）| A． | 3月份 | B． | 4月份 | C． | 5月份 | D． | 6月份 |
4．
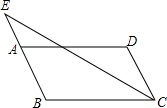如图，在?ABCD中，AB=3，AD=5，∠BCD的平分线交BA的延长线于点E，则AE的长为（ ）
如图，在?ABCD中，AB=3，AD=5，∠BCD的平分线交BA的延长线于点E，则AE的长为（ ）| A． | 3 | B． | 2.5 | C． | 2 | D． | 1.5 |
11．
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究，探究过程如下，请补充完整．
（1）自变量x的取值范围是全体实数，x与y的几组对应值列表如下：
其中，m=0．
（2）根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分．
（3）观察函数图象，写出两条函数的性质．
（4）进一步探究函数图象发现：
①函数图象与x轴有3个交点，所以对应的方程x2-2|x|=0有3个实数根；
②方程x2-2|x|=2有2个实数根；
③关于x的方程x2-2|x|=a有4个实数根时，a的取值范围是-1＜a＜0．
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究，探究过程如下，请补充完整．（1）自变量x的取值范围是全体实数，x与y的几组对应值列表如下：
| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | 3 | $\frac{5}{4}$ | m | -1 | 0 | -1 | 0 | $\frac{5}{4}$ | 3 | … |
（2）根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分．
（3）观察函数图象，写出两条函数的性质．
（4）进一步探究函数图象发现：
①函数图象与x轴有3个交点，所以对应的方程x2-2|x|=0有3个实数根；
②方程x2-2|x|=2有2个实数根；
③关于x的方程x2-2|x|=a有4个实数根时，a的取值范围是-1＜a＜0．
8．
2016年里约热内卢奥运会（即第31届夏季奥林匹克运动会）开幕式将于当地时间8月5日在马拉卡纳体育场举行．如图是第31届夏季奥林匹克运动会会徽图案，下列关于它的对称性判定正确的是（ ）
2016年里约热内卢奥运会（即第31届夏季奥林匹克运动会）开幕式将于当地时间8月5日在马拉卡纳体育场举行．如图是第31届夏季奥林匹克运动会会徽图案，下列关于它的对称性判定正确的是（ ）| A． | 只是轴对称图形 | |
| B． | 只是中心对称图形 | |
| C． | 既不是轴对称图形也不是中心对称图形 | |
| D． | 既是轴对称图形也是中心对称图形 |