题目内容
5.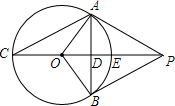 如图,PA,PB分别切⊙O于点A,B,作射线PO,分别交⊙O于点E,C,交AB于点D,∠C=30°,PO=12.
如图,PA,PB分别切⊙O于点A,B,作射线PO,分别交⊙O于点E,C,交AB于点D,∠C=30°,PO=12.(1)求点P到⊙O的切线PA的长;
(2)求△AOB的面积.
分析 (1)根据等腰三角形的性质得到∠AOP=60°,根据PA,PB分别切⊙O于点A,B,得到∠OAP=90°,于是得到OA=$\frac{1}{2}$OP=6,根据勾股定理即可得到结果;
(2)根据PA,PB分别切⊙O于点A,B,得到PA=PB,∠APO=∠BPO,根据等腰三角形的性质得到AB⊥OP,求得OD=$\frac{1}{2}$OA=3,AD=3$\sqrt{3}$,根据三角形的面积公式即可得到结论.
解答 解:(1)∵OA=OC,∠C=30°,
∴∠AOP=60°,
∵PA,PB分别切⊙O于点A,B,
∴∠OAP=90°,
∴∠APO=30°,
∵PO=12,
∴OA=$\frac{1}{2}$OP=6,
∴PA=$\sqrt{O{P}^{2}-O{A}^{2}}$=6$\sqrt{3}$;
(2)∵PA,PB分别切⊙O于点A,B,
∴PA=PB,∠APO=∠BPO,
∴AB⊥OP,
∴OD=$\frac{1}{2}$OA=3,AD=3$\sqrt{3}$,
∴AB=2AD=6$\sqrt{3}$,
∴S△AOB=$\frac{1}{2}$×6$\sqrt{3}$×3=9$\sqrt{3}$.
点评 本题考查了切线的性质,直角三角形的性质,勾股定理,熟练掌握切线的性质定理是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
15.下列叙述正确的是( )
| A. | 如果a存在平方根,则a>0 | B. | $\sqrt{16}$=±4 | ||
| C. | $\sqrt{5}$是5的一个平方根 | D. | 5的平方根是$\sqrt{5}$ |
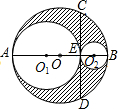 如图,AB是⊙O的直径,弦CD⊥AB于E,分别以AE、BE为直径作两个大小不同的⊙O1和⊙O2,若CD=16,则图中阴影部分的面积为32π(结果保留π).
如图,AB是⊙O的直径,弦CD⊥AB于E,分别以AE、BE为直径作两个大小不同的⊙O1和⊙O2,若CD=16,则图中阴影部分的面积为32π(结果保留π).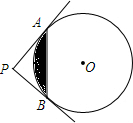 如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.
如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积. 阅读下题及其证明过程.
阅读下题及其证明过程.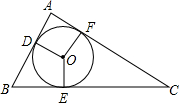 如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.
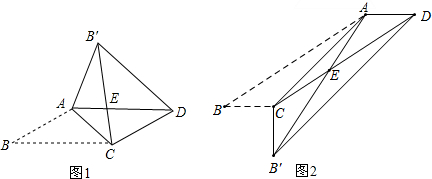
如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.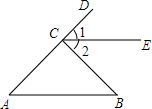 如图,已知∠A=∠B,点A,C,D在同一条直线上,∠DCB=∠A+∠B,CE是∠DCB的平分线,试说明CE∥AB.
如图,已知∠A=∠B,点A,C,D在同一条直线上,∠DCB=∠A+∠B,CE是∠DCB的平分线,试说明CE∥AB.