题目内容
20.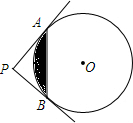 如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.
如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.
分析 连接OA、OB,PA,由于PA、PB分别切⊙O于点A、B,于是得到∠PAO=∠PBO=90°,PA=PB,推出四边形APBO是正方形,根据正方形的性质得到OA=OB=PA=4,∠AOB=90°,根据扇形和三角形的面积公式即可得到结论.
解答 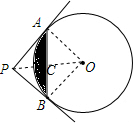 解:连接OA、OB,PA,
解:连接OA、OB,PA,
∵PA、PB分别切⊙O于点A、B,
∴∠PAO=∠PBO=90°,PA=PB,
∵PA⊥PB于点P,
∴四边形APBO是正方形,
∴OA=OB=PA=4,∠AOB=90°,
∴S阴影=S扇形AOB-S△AOB=$\frac{90π•{4}^{2}}{360}$-$\frac{1}{2}×4×4$=4π-8.
点评 本题考查了切线的性质及扇形的面积计算方法,正方形的判定和性质,证得四边形APBO是正方形是解题的关键.

练习册系列答案
相关题目
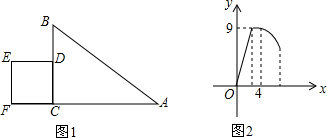

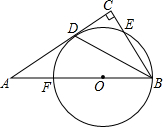 已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.
已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.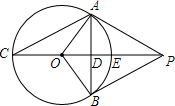 如图,PA,PB分别切⊙O于点A,B,作射线PO,分别交⊙O于点E,C,交AB于点D,∠C=30°,PO=12.
如图,PA,PB分别切⊙O于点A,B,作射线PO,分别交⊙O于点E,C,交AB于点D,∠C=30°,PO=12.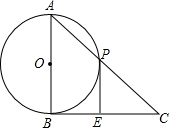 已知:如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点P,点E在BC上,并且PE切⊙O于点P.求证:CE=BE.
已知:如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点P,点E在BC上,并且PE切⊙O于点P.求证:CE=BE.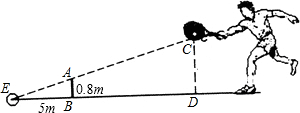 如图,小明打网球时能击中球的最高高度CD是2.4m,如果发球时要使球恰好能打过网AB,且落在离网5m的位置上,那么小明在离网多远的位置发球?
如图,小明打网球时能击中球的最高高度CD是2.4m,如果发球时要使球恰好能打过网AB,且落在离网5m的位置上,那么小明在离网多远的位置发球?