题目内容
13.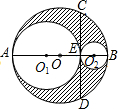 如图,AB是⊙O的直径,弦CD⊥AB于E,分别以AE、BE为直径作两个大小不同的⊙O1和⊙O2,若CD=16,则图中阴影部分的面积为32π(结果保留π).
如图,AB是⊙O的直径,弦CD⊥AB于E,分别以AE、BE为直径作两个大小不同的⊙O1和⊙O2,若CD=16,则图中阴影部分的面积为32π(结果保留π).
分析 连接CA,DA,根据垂径定理得到CE=ED=8,根据圆周角定理得到∠ACB=90°,易证Rt△ECA∽Rt△EBD,则EC2=EA•EB=100;利用S阴影部分=S⊙O-S⊙1-S⊙2和圆的面积公式进行变形可得到阴影部分的面积=$\frac{1}{2}$•AE•EB•π,即可计算出阴影部分的面积.
解答 解:连接CA,DA,如图: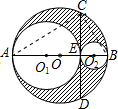
∵AB⊥CD,CD=16,
∴CE=DE=8,
又∵AB为直径,
∴∠ACB=90°,
∴∠CEA=∠BEC=90°,
∴∠A+∠ACE=90°,∠A+∠B=90°,
∴∠ACE=∠B,
∴Rt△ECA∽Rt△EBC,
∴EC:EB=EA:EC,
∴EC2=EA•EB=64;
S阴影部分=S⊙O-S⊙1-S⊙2
=π•$\frac{1}{4}$AB2-π•$\frac{1}{4}$AE2-π•$\frac{1}{4}$BE2
=π[$\frac{1}{4}$AB2-$\frac{1}{4}$AE2-$\frac{1}{4}$(AB-AE)2]
=π($\frac{1}{2}$AE•AB-$\frac{1}{2}$AE2)
=$\frac{1}{2}$•AE•EB•π
=32π.
故答案为:32π.
点评 本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧;也考查了圆周角定理和三角形相似的判定与性质以及圆的面积公式.

练习册系列答案
相关题目


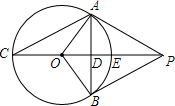 如图,PA,PB分别切⊙O于点A,B,作射线PO,分别交⊙O于点E,C,交AB于点D,∠C=30°,PO=12.
如图,PA,PB分别切⊙O于点A,B,作射线PO,分别交⊙O于点E,C,交AB于点D,∠C=30°,PO=12.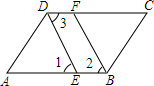 如图.∠1=∠2,∠2=∠3.你能判断图中哪些直线平行.并说明理由.
如图.∠1=∠2,∠2=∠3.你能判断图中哪些直线平行.并说明理由.