题目内容
15.【发现与证明】把平行四边形沿着它的一条对角线翻折,会发现这其中有许多结论:?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,AD 与B′C交于E,连结B′D,则△A B′C与?ABCD重叠部分的图形(△AEC)是等腰三角形.请利用图1证明这个结论.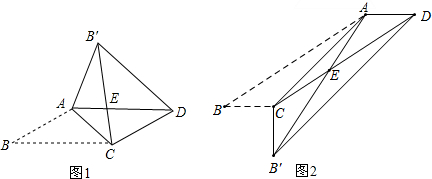
【应用与探究】
(1)如图1,已知∠B=30°,若AB=$\sqrt{3}$,∠AB′D=75°,则∠ACB=45°°;
(2)如图2,已知∠B=30°,AB=2$\sqrt{3}$,BC=1,AB′与边CD相交于点E,求△AEC的面积.
分析 (1)△ABC沿AC翻折至△AB′C,∠B=30°得到∠AB′C=∠B=30°,即∠ACB=∠CB′D=∠AB′D-∠AB′C=∠AB′D-∠B=75°-30°=45°
(2)过C点分别作CG⊥AB,CH⊥A B′,垂足分别为G、H,应用含30度直角三角形的性质和勾股定理AE和CH的长即可求出△AEC的面积.
解答 【发现与证明】解:如答图1,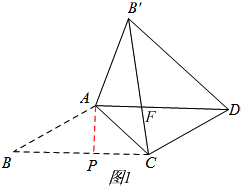
设AD与B′C相交于点F,
∵△ABC沿AC翻折至△AB′C,
∴△ABC≌△△AB′C,∠ACB=∠ACB′,BC=B′C.
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴B′C=AD,∠ACB=∠CAD.
∴∠ACB′=∠CAD=$\frac{180°-∠B′FD}{2}$
∴AF=CF.
∴B′F=DF.
∴∠CB′D=∠B′DA=$\frac{180°-∠B′FD}{2}$
∵∠AFC=∠B′FD,
∴∠ACB′=∠CB′D
∴B′D∥AC.
【应用与探究】
(1)设AD与B′C相交于点F,
∵△ABC沿AC翻折至△AB′C,
∴△ABC≌△△AB′C,∠ACB=∠ACB′,BC=B′C.
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴B′C=AD,∠ACB=∠CAD.
∴∠ACB′=∠CAD=$\frac{180°-∠B′FD}{2}$
∴AF=CF.
∴B′F=DF.
∴∠CB′D=∠B′DA=$\frac{180°-∠B′FD}{2}$
∵∠AFC=∠B′FD,
∴∠ACB′=∠CB′D
∴∠ACB=∠CB′D=∠AB′D-∠AB′C=∠AB′D-∠B=75°-30°=45°,
故答案为45°
(2)如答图2,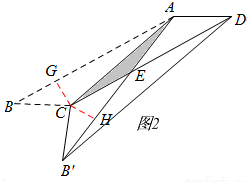
过C点分别作CG⊥AB,CH⊥AB′,垂足分别为G、H.
∴CG=CH.
在Rt△BCG中,∠BGC=90°,BC=1,∠B=30°,
∴CG=$\frac{1}{2}$,BG=$\frac{\sqrt{3}}{2}$
∵AB=2$\sqrt{3}$,
∴AC=$\frac{3\sqrt{3}}{2}$
∵△AGC≌△AHC,
∴CH=CG=$\frac{1}{2}$,AH=AG=$\frac{3\sqrt{3}}{2}$
设AE=CE=x,
由勾股定理得,CE2=CH2+HE2
即:x2=($\frac{1}{2}$)2+($\frac{3\sqrt{3}}{2}$-x)2,
∴x=$\frac{7\sqrt{3}}{9}$
∴△AEC的面积=$\frac{1}{2}$AE×CH=$\frac{7\sqrt{3}}{36}$.
点评 此题是几何变换综合题,本题主要考查了翻折变换的性质及其应用问题;计算和表示出角和线段是解本题的关键.

 一次函数y=kx+b(k,b是常数,k≠0)图象如图所示,则不等式kx+b>0的解集是x>-2.
一次函数y=kx+b(k,b是常数,k≠0)图象如图所示,则不等式kx+b>0的解集是x>-2.
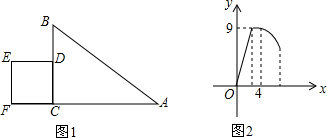
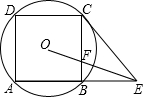 如图,四边形ABCD是⊙O的内接正方形,延长AB至点P,使BP=AB,连接PC.
如图,四边形ABCD是⊙O的内接正方形,延长AB至点P,使BP=AB,连接PC. 如图,AB是⊙O的直径,点C、D在⊙O上,且AC平分∠BAD,点E为AB的延长线上一点,且∠ECB=∠CAD.
如图,AB是⊙O的直径,点C、D在⊙O上,且AC平分∠BAD,点E为AB的延长线上一点,且∠ECB=∠CAD.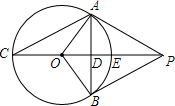 如图,PA,PB分别切⊙O于点A,B,作射线PO,分别交⊙O于点E,C,交AB于点D,∠C=30°,PO=12.
如图,PA,PB分别切⊙O于点A,B,作射线PO,分别交⊙O于点E,C,交AB于点D,∠C=30°,PO=12.