题目内容
14.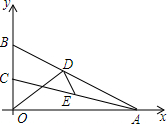 如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 作AC关于AB的对称线AC′,根据三角形的内角和得到∠CAO=10°,∠BAO=20°,得到∠C′AO=30°,作OF⊥AC′交AC′于F,交AB于D,过D作DE⊥AC于E,则OF的长即为OD+OE的最小值,根据直角三角形的性质即可得到结论.
解答 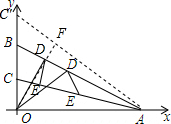 解:作AC关于AB的对称线AC′,
解:作AC关于AB的对称线AC′,
∵∠ACO=80°,
∴∠CAO=10°,
∵∠ABO=70°,
∴∠BAO=20°,
∴∠C′AO=30°,
作OF⊥AC′交AC′于F,交AB于D,过D作DE⊥AC于E,则OF的长即为OD+OE的最小值,
∴OF=$\frac{1}{2}$OA=4,
∴OD+DE的最小值等于4,
故选A.
点评 本题考查了轴对称-最短路线问题,坐标与图形的性质,正确的作出图形是解题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
7.已知关于x的一元二次方程x2+$\sqrt{k-1}$x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-7 | B. | k≥-7 | C. | k≥0 | D. | k≥1 |
 某校中考模拟试题中有这样一道试题:
某校中考模拟试题中有这样一道试题: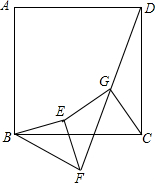 已知正方形ABCD,△BEF是等腰直角三角形(BE=EF),联结FD,在FD上取中点G,联结EC和CG,求证:
已知正方形ABCD,△BEF是等腰直角三角形(BE=EF),联结FD,在FD上取中点G,联结EC和CG,求证: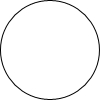 △ABC内接于⊙O,∠B=60°,AC=2cm,⊙O的直径为多少?
△ABC内接于⊙O,∠B=60°,AC=2cm,⊙O的直径为多少?