题目内容
8.解关于x、y的二元二次方程$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=20}\\{{x}^{2}-4xy+4{y}^{2}=0}\end{array}\right.$.分析 由x2-4xy+4y2=0可得x=2y,代入x2+y2=20,可求出y,从而可求出x,问题得以解决.
解答 解:由x2-4xy+4y2=0得(x-2y)2=0,
则x=2y.
把x=2y代入x2+y2=20,得
5y2=20,
解得y=±2.
当y=2时x=4;
当y=-2时x=-4;
故原方程组的解为$\left\{\begin{array}{l}{{x}_{1}=4}\\{{y}_{1}=2}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}=-4}\\{{y}_{2}=-2}\end{array}\right.$.
点评 本题主要考查的是二元二次方程组的解法、完全平方公式、代入消元法、解一元二次方程等知识,运用代入消元法是解决本题的关键.

练习册系列答案
相关题目
18.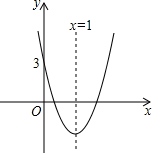 如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
①b2-4ac<0,②abc<0,③4a+2b+c=1,④a-b+c>0中,判断正确的有( )
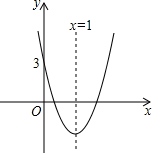 如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:①b2-4ac<0,②abc<0,③4a+2b+c=1,④a-b+c>0中,判断正确的有( )
| A. | ②③④ | B. | ①②③ | C. | ②③ | D. | ①④ |

 如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点也在抛物线C1上,那么我们称抛物线C1与C2关联.
如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点也在抛物线C1上,那么我们称抛物线C1与C2关联.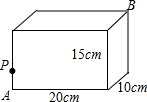 如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少?
如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少?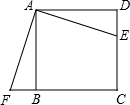 如图,E是正方形ABCD的边CD上一点,F是CB延长线上一点,且AF⊥EA,说明△ABF≌△ADE的理由.
如图,E是正方形ABCD的边CD上一点,F是CB延长线上一点,且AF⊥EA,说明△ABF≌△ADE的理由.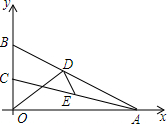 如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )