题目内容
6. △ABC内接于⊙O,∠B=60°,AC=2cm,⊙O的直径为多少?
△ABC内接于⊙O,∠B=60°,AC=2cm,⊙O的直径为多少?
分析 作直径AD,连接CD,由圆周角定理得出∠D=∠B=60°,∠ACD=90°,由三角函数求出AD,即可得出结果.
解答 解:如图所示:
作直径AD,连接CD,
则∠D=∠B=60°,∠ACD=90°,
∴AD=$\frac{AC}{sinD}$=$\frac{2}{\frac{\sqrt{3}}{2}}$=$\frac{4\sqrt{3}}{3}$,
即⊙O的直径为$\frac{4\sqrt{3}}{3}$.
点评 本题考查了三角形的外接圆、圆周角定理、三角函数;熟练掌握圆周角定理是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.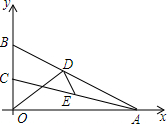 如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
 如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
11.使分式$\frac{{x}^{2}+1}{1-2x}$的值为负的x的取值范围是( )
| A. | x<0 | B. | x<$\frac{1}{2}$ | C. | x$≥\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
18.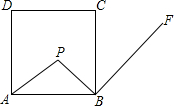 如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
 如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )| A. | 2或$\frac{25}{2}$ | B. | 2 | C. | $\frac{25}{2}$ | D. | 2或$\frac{15}{2}$ |
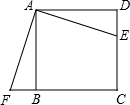 如图,E是正方形ABCD的边CD上一点,F是CB延长线上一点,且AF⊥EA,说明△ABF≌△ADE的理由.
如图,E是正方形ABCD的边CD上一点,F是CB延长线上一点,且AF⊥EA,说明△ABF≌△ADE的理由. 如图,△ABC中,AB=AC=16cm,AB的垂直平分线ED交AC于D点.
如图,△ABC中,AB=AC=16cm,AB的垂直平分线ED交AC于D点.