题目内容
7.已知关于x的一元二次方程x2+$\sqrt{k-1}$x-1=0有两个不相等的实数根,则k的取值范围是( )| A. | k>-7 | B. | k≥-7 | C. | k≥0 | D. | k≥1 |
分析 根据方程有两个不相等的实数根可知△>0,再由二次根式有意义的条件得出k-1≥0,求出k的取值范围即可.
解答 解:∵关于x的一元二次方程x2+$\sqrt{k-1}$x-1=0有两个不相等的实数根,
∴$\left\{\begin{array}{l}△=(\sqrt{k-1})^{2}+4>0\\ k-1≥0\end{array}\right.$,
解得k≥1.
故选D.
点评 本题考查的是根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系是解答此题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
18.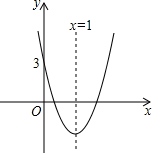 如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
①b2-4ac<0,②abc<0,③4a+2b+c=1,④a-b+c>0中,判断正确的有( )
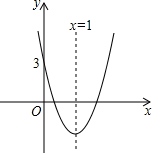 如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:①b2-4ac<0,②abc<0,③4a+2b+c=1,④a-b+c>0中,判断正确的有( )
| A. | ②③④ | B. | ①②③ | C. | ②③ | D. | ①④ |
15.若关于x的一元二次方程(m+1)x2-2x+1=0有实数根,则实数m的取值范围是( )
| A. | m≥0 | B. | m≤0 | C. | m≠1 | D. | m≤0且m≠-1 |
12.使得二次根式$\sqrt{3-4x}$有意义的字母x的取值范围是( )
| A. | x≥$\frac{3}{4}$ | B. | x≤$\frac{3}{4}$ | C. | x<$\frac{3}{4}$ | D. | x≠$\frac{3}{4}$ |
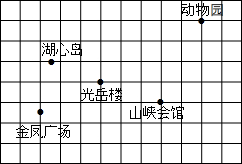 如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置.
如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置. 已知:如图,在?ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.求证:△DOE≌△BOF.
已知:如图,在?ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.求证:△DOE≌△BOF.
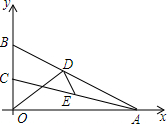 如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )