题目内容
3．化简：$\frac{a-b}{a+b}$+$\frac{b-c}{b+c}$+$\frac{c-a}{c+a}$+$\frac{（a-b）（b-c）（c-a）}{（a+b）（b+c）（c+a）}$．分析 根据所求的式子先通分，再化简即可解答本题．
解答 解：$\frac{a-b}{a+b}$+$\frac{b-c}{b+c}$+$\frac{c-a}{c+a}$+$\frac{（a-b）（b-c）（c-a）}{（a+b）（b+c）（c+a）}$
=$\frac{（a-b）（b+c）（c+a）+（b-c）（a+b）（c+a）+（c-a）（a+b）（b+c）}{（a+b）（b+c）（c+a）}$+$\frac{（a-b）（b-c）（c-a）}{（a+b）（b+c）（c+a）}$
=$\frac{（c+a）[（a-b）（b+c）+（b-c）（a+b）]+（c-a）[（a+b）（b+c）+（a-b）（b-c）]}{（a+b）（b+c）（c+a）}$
=$\frac{2b（c+a）（a-c）+2b（c-a）（c+a）}{（a+b）（b+c）（c+a）}$
=0．
点评 本题考查分式的加减法，解题的关键是明确分式加减法的计算方法．
练习册系列答案
相关题目
14．
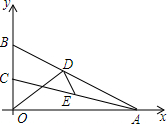如图，在平面直角坐标系xOy中，已知点A（8，0），点B、C在y轴的正半轴上，且∠ABO=70°，∠ACO=80°，点D、E分别是线段AB、AC上的动点，则线段OD+DE的最小值等于（ ）
如图，在平面直角坐标系xOy中，已知点A（8，0），点B、C在y轴的正半轴上，且∠ABO=70°，∠ACO=80°，点D、E分别是线段AB、AC上的动点，则线段OD+DE的最小值等于（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
11．使分式$\frac{{x}^{2}+1}{1-2x}$的值为负的x的取值范围是（ ）
| A． | x＜0 | B． | x＜$\frac{1}{2}$ | C． | x$≥\frac{1}{2}$ | D． | x$＞\frac{1}{2}$ |
18．
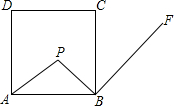如图，点P是边长为5的正方形ABCD内一点，且PB=2，PB⊥BF，垂足为点B，请在射线BF上找一点M，使得以B，M，C为顶点的三角形与△ABP相似，则BM等于（ ）
如图，点P是边长为5的正方形ABCD内一点，且PB=2，PB⊥BF，垂足为点B，请在射线BF上找一点M，使得以B，M，C为顶点的三角形与△ABP相似，则BM等于（ ）| A． | 2或$\frac{25}{2}$ | B． | 2 | C． | $\frac{25}{2}$ | D． | 2或$\frac{15}{2}$ |
8．关于x的分式方程$\frac{3}{x}$+$\frac{6}{x-1}$-$\frac{x+k}{x（x-1）}$=0有解，则k满足（ ）
| A． | k≠-3 | B． | k≠5 | C． | k≠-3且k≠-5 | D． | k≠-3且k≠5 |
如图，△ABC中，AB=AC，E、F、G分别是BC、AB、AC上一点，∠FEG=2∠B．