题目内容
4．己知$\frac{1}{x}$-$\frac{1}{y}$=5，求分式$\frac{3x+5xy-3y}{x-3xy-y}$的值．分析 首先将已知变形进而得出x-y=-5xy，再代入原式求出答案．
解答 解：∵$\frac{1}{x}$-$\frac{1}{y}$=5，
∴$\frac{y-x}{xy}$=5，
∴x-y=-5xy
则$\frac{3x+5xy-3y}{x-3xy-y}$=$\frac{3（x-y）+5xy}{（x-y）-3xy}$=$\frac{-15xy+5xy}{-5xy-3xy}$=$\frac{5}{4}$．
点评 此题主要考查了分式的值，正确将已知变形进而化简是解题关键．
练习册系列答案
相关题目
14．
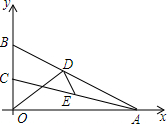如图，在平面直角坐标系xOy中，已知点A（8，0），点B、C在y轴的正半轴上，且∠ABO=70°，∠ACO=80°，点D、E分别是线段AB、AC上的动点，则线段OD+DE的最小值等于（ ）
如图，在平面直角坐标系xOy中，已知点A（8，0），点B、C在y轴的正半轴上，且∠ABO=70°，∠ACO=80°，点D、E分别是线段AB、AC上的动点，则线段OD+DE的最小值等于（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
如图，△ABC中，AB=AC，E、F、G分别是BC、AB、AC上一点，∠FEG=2∠B．
19．计算$\frac{\sqrt{5}a}{\sqrt{10a}}$得到的最后结果是（ ）
| A． | $\frac{\sqrt{a}}{\sqrt{2}}$ | B． | $\frac{\sqrt{2a}}{2}$ | C． | $\sqrt{\frac{a}{2}}$ | D． | $\sqrt{\frac{2a}{2}}$ |
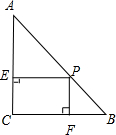已知△ABC中，AC=BC=3$\sqrt{2}$，∠C=90°，AB上有一动点P，过点P作PE⊥AC于E，PF⊥BC于F．