题目内容
9.化简$\frac{{x}^{2}}{x+1}$+$\frac{1}{x}$的结果是$\frac{{x}^{3}+x+1}{x(x+1)}$.分析 直接通分运算进而求出答案.
解答 解:$\frac{{x}^{2}}{x+1}$+$\frac{1}{x}$
=$\frac{{x}^{3}}{x(x+1)}$+$\frac{x+1}{x(x+1)}$
=$\frac{{x}^{3}+x+1}{x(x+1)}$.
故答案为:$\frac{{x}^{3}+x+1}{x(x+1)}$.
点评 此题主要考查了分式的加减运算,正确通分是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
14.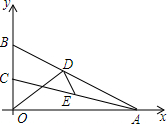 如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
 如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
18.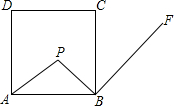 如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
 如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )| A. | 2或$\frac{25}{2}$ | B. | 2 | C. | $\frac{25}{2}$ | D. | 2或$\frac{15}{2}$ |
19.计算$\frac{\sqrt{5}a}{\sqrt{10a}}$得到的最后结果是( )
| A. | $\frac{\sqrt{a}}{\sqrt{2}}$ | B. | $\frac{\sqrt{2a}}{2}$ | C. | $\sqrt{\frac{a}{2}}$ | D. | $\sqrt{\frac{2a}{2}}$ |
 已知:如图,在?ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.求证:△DOE≌△BOF.
已知:如图,在?ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.求证:△DOE≌△BOF. 如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点也在抛物线C1上,那么我们称抛物线C1与C2关联.
如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点也在抛物线C1上,那么我们称抛物线C1与C2关联.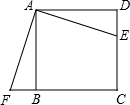 如图,E是正方形ABCD的边CD上一点,F是CB延长线上一点,且AF⊥EA,说明△ABF≌△ADE的理由.
如图,E是正方形ABCD的边CD上一点,F是CB延长线上一点,且AF⊥EA,说明△ABF≌△ADE的理由.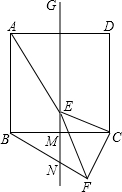 已知如图,正方形ABCD中,GM是其对称轴,E点是线段GM上的点,连接CE,以CE为直角边作等腰直角三角形CEF,∠ECF=90°,连接FB交直线GM于N
已知如图,正方形ABCD中,GM是其对称轴,E点是线段GM上的点,连接CE,以CE为直角边作等腰直角三角形CEF,∠ECF=90°,连接FB交直线GM于N 如图,△ABC中,AB=AC=16cm,AB的垂直平分线ED交AC于D点.
如图,△ABC中,AB=AC=16cm,AB的垂直平分线ED交AC于D点.