题目内容
 如图,AD为△ABC的中线,
如图,AD为△ABC的中线,(1)作△ABD的中线BE;
(2)作△BED的BD边上的高EF;
(3)若△ABC的面积为60,BD=10,则点E到BC边的距离为多少?
考点:作图—复杂作图,点到直线的距离
专题:
分析:(1)找到AD的中点E,进而得出答案;
(2)过点E作EF⊥BC交BC于点F即可;
(3)利用三角形中线平分三角形面积进而得出答案.
(2)过点E作EF⊥BC交BC于点F即可;
(3)利用三角形中线平分三角形面积进而得出答案.
解答: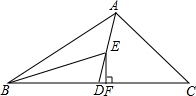 解:(1)如图所示:BE即为所求;
解:(1)如图所示:BE即为所求;
(2)如图所示:BD边上的高EF;
(3)∵AD为△ABC的中线,△ABC的面积为60,
∴△ABD的面积为30,
∵△ABD的中线BE,
∴△BDE的面积为:15,
∴
×EF×BD=15,
∴
×EF×10=15,
解得:EF=3,
则点E到BC边的距离为3.
 解:(1)如图所示:BE即为所求;
解:(1)如图所示:BE即为所求;(2)如图所示:BD边上的高EF;
(3)∵AD为△ABC的中线,△ABC的面积为60,
∴△ABD的面积为30,
∵△ABD的中线BE,
∴△BDE的面积为:15,
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得:EF=3,
则点E到BC边的距离为3.
点评:此题主要考查了三角形中线画法以及高线画法和三角形中线的性质等知识,熟练利用三角形中线平分三角形面积是解题关键.

练习册系列答案
相关题目
 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=45°.∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=45°.∠B′=110°,则∠BCA′的度数是( )| A、55° | B、75° |
| C、95° | D、110° |
 在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F. 如图,在等边三角形ABC中,AB=6,D是BC的中点,将△ABD按逆时针方向旋转后得△ACE.
如图,在等边三角形ABC中,AB=6,D是BC的中点,将△ABD按逆时针方向旋转后得△ACE. 如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.试证明:无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的
如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.试证明:无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的