题目内容
 在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.(1)求证:四边形BFDE为平行四边形;
(2)探究:当∠CBD的度数为多少度时四边形BFDE为菱形,并给予证明,求出此时AB:BC的值.
考点:翻折变换(折叠问题),平行四边形的判定,菱形的判定
专题:
分析:(1)利用矩形性质得出∠ABE=∠CDF,∠EBD=∠FDB,进而得出△ABE≌△CDF,即可得出EB∥DF,EB=DF,即可得出答案;
(2)根据矩形的性质,可得∠A=∠ABC=90°,根据角的和差,可得∠ABE的度数,根据折叠,可得∠ABE与∠EBD的关系,根据平行线的性质,可得∠EBD与∠FDB的关系,根据等腰三角形的判定,可得BF与DE的关系,可得证明结论;根据特殊角的正切值,可得答案.
(2)根据矩形的性质,可得∠A=∠ABC=90°,根据角的和差,可得∠ABE的度数,根据折叠,可得∠ABE与∠EBD的关系,根据平行线的性质,可得∠EBD与∠FDB的关系,根据等腰三角形的判定,可得BF与DE的关系,可得证明结论;根据特殊角的正切值,可得答案.
解答:(1)证明:∵四边形ABCD为矩形,
∴AB∥CD,AB=CD,∠A=∠C.
∴∠ABD=∠CDB,
由翻折知,∠ABE=∠EBD=
∠ABD,∠CDF=∠FDB=
∠CDB,
∴∠ABE=∠CDF,∠EBD=∠FDB,
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA),
∴EB=DF,
∵∠EBD=∠FDB,
∴EB∥DF,
∴四边形EBFD为平行四边形;
(2)当∠CBD=30°时四边形BFDE为菱形,
证明:∵ABCD是矩形,
∴∠ABC=90°.
∠CBD=30°,
∴∠ABD=60°.
∵折叠的性质
∴∠ABE=∠EBD=30°,
四边形BFDE为平行四边形
∴BE∥DF,
∠FDB=∠EBD=30°,
∴∠FBD=∠FDB,
∴BF=DF
∴四边形BFDE为菱形;
tan∠DBC=tan30°=
=
=
,
∴
=
.
∴AB∥CD,AB=CD,∠A=∠C.
∴∠ABD=∠CDB,
由翻折知,∠ABE=∠EBD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABE=∠CDF,∠EBD=∠FDB,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(ASA),
∴EB=DF,
∵∠EBD=∠FDB,
∴EB∥DF,
∴四边形EBFD为平行四边形;
(2)当∠CBD=30°时四边形BFDE为菱形,
证明:∵ABCD是矩形,
∴∠ABC=90°.
∠CBD=30°,
∴∠ABD=60°.
∵折叠的性质
∴∠ABE=∠EBD=30°,
四边形BFDE为平行四边形
∴BE∥DF,
∠FDB=∠EBD=30°,
∴∠FBD=∠FDB,
∴BF=DF
∴四边形BFDE为菱形;
tan∠DBC=tan30°=
| DC |
| BC |
| AB |
| BC |
| ||
| 3 |
∴
| AB |
| BC |
| ||
| 3 |
点评:本题主要考查了折叠问题,矩形的性质以及全等三角形的判定与性质和平行四边形的判定等知识,根据已知得出△ABE≌△CDF是解题关键;一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
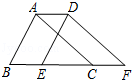 如图,将周长为7的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为7的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )| A、8 | B、9 | C、10 | D、11 |
两整式乘积结果为a2+7a+12的是( )
| A、(a+3)(a-4) |
| B、(a+3)(a+4) |
| C、(a+6)(a-2) |
| D、(a-6)(a+2) |


 如图,AD为△ABC的中线,
如图,AD为△ABC的中线,