题目内容
 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=45°.∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=45°.∠B′=110°,则∠BCA′的度数是( )| A、55° | B、75° |
| C、95° | D、110° |
考点:旋转的性质
专题:
分析:根据旋转的性质可得∠B=∠B′,然后利用三角形内角和定理列式求出∠ACB,再根据对应边AC、A′C的夹角为旋转角求出∠ACA′,然后根据∠BCA′=∠ACB+∠ACA′计算即可得解.
解答:解:∵△ABC绕着点C顺时针旋转50°后得到△A′B′C′,
∴∠B=∠B′=110°,∠ACA′=50°,
在△ABC中,∠ACB=180°-∠A-∠B=180°-45°-110°=25°,
∴∠BCA′=∠ACB+∠ACA′=50°+25°=75°.
故选B.
∴∠B=∠B′=110°,∠ACA′=50°,
在△ABC中,∠ACB=180°-∠A-∠B=180°-45°-110°=25°,
∴∠BCA′=∠ACB+∠ACA′=50°+25°=75°.
故选B.
点评:本题考查了旋转的性质,三角形的内角和定理,熟记旋转变换的对应的角相等,以及旋转角的确定是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
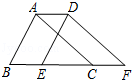 如图,将周长为7的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为7的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )| A、8 | B、9 | C、10 | D、11 |
中华人民共和国国旗上的五角星,它的五个锐角的度数和是( )
| A、50° | B、100° |
| C、180° | D、200° |
下列各式中能用平方差公式分解的是( )
| A、x2+4y2 |
| B、-x2-4y2 |
| C、x2-2y2+1 |
| D、x2-4y2 |
关于x,y的方程组
的解满足x+y=6,则m的值为( )
|
| A、1 | B、2 | C、3 | D、4 |
两整式乘积结果为a2+7a+12的是( )
| A、(a+3)(a-4) |
| B、(a+3)(a+4) |
| C、(a+6)(a-2) |
| D、(a-6)(a+2) |

 如图,AD为△ABC的中线,
如图,AD为△ABC的中线,