题目内容
8.已知二次函数y=ax2-4ax+3a的图象经过点(0,3).(1)求a的值;
(2)将该函数的图象沿y轴翻折,求翻折后所得图象的函数表达式.
分析 (1)代入(0,3)点,根据待定系数法即可求得;
(2)根据抛物线的解析式求得顶点坐标,然后求得翻折后图象的顶点坐标,设成顶点式,代入(0,3),根据待定系数法即可求得.
解答 解:(1)∵二次函数y=ax2-4ax+3a的图象经过点(0,3),
∴3=3a.
解得a=1.
(2)∵y=x2-4x+3=(x-2)2-1.
∴图象的顶点坐标为(2,-1).
∴翻折后图象的顶点坐标为(-2,-1).
设新函数的表达式为y=b(x+2)2-1.
由题意得新函数的图象经过点(0,3),
∴3=b•22-1.
解得b=1.
∴新函数的表达式为y=(x+2)2-1(或y=x2+4x+3).
点评 本题考查了待定系数法求二次函数的解析式,对折的性质以及二次函数的性质,求得对折后的顶点坐标是解题的关键.

练习册系列答案
相关题目
 如图,在一块△ABC板面中,将△BEF涂黑,其中点D、E、F分别为BC、AD、CE的中点,小华随意向△ABC板面内部射击一粒小弹丸,则弹丸击中黑色区域的概率是( )
如图,在一块△ABC板面中,将△BEF涂黑,其中点D、E、F分别为BC、AD、CE的中点,小华随意向△ABC板面内部射击一粒小弹丸,则弹丸击中黑色区域的概率是( )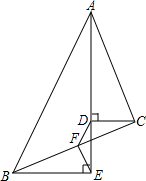 如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连结DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是$\sqrt{2}$.
如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连结DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是$\sqrt{2}$.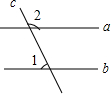 如图,直线a∥b,直线c与a,b相交,∠1=55°,则∠2=125°.
如图,直线a∥b,直线c与a,b相交,∠1=55°,则∠2=125°.