题目内容
18．观察下列各式：（x-1）（x+1）=x2-1
（x-1）（x2+x+1）=x3-1
（x-1）（x3+x2+x+1）=x4-1
（x-1）（x4+x3+x2+x+1）=x5-1
（1）写出第5个式子：（x-1）（x5+x4+x3+x2+x+1）=x6-1．
（2）根据前面各式的规律可得：（x-1）（xn+xn-1+…+x+1）=xn+1-1． （其中n为正整数）
（3）根据（2）求1+2+22+23+…+262+263的值=264-1，并求出它的个位数字=5．
分析 （1）仿照已知等式得出第5个等式即可；
（2）归纳总结得到一般性规律，写出即可；
（3）根据得出的规律将原式变形，计算得到结果，即可做出判断．
解答 解：（1）写出第5个式子：（x-1）（x5+x4+x3+x2+x+1）=x6-1；
（2）根据前面各式的规律可得：（x-1）（xn+xn-1+…+x+1）=xn+1-1；（其中n为正整数）
（3）根据（2）求1+2+22+23+…+262+263=（2-1）（1+2+22+23+…+262+263）=264-1，并求出它的个位数字=5，
故答案为：（1）（x-1）（x5+x4+x3+x2+x+1），x6-1；（2）xn+1-1；（3）264-1，5
点评 此题考查了平方差公式，弄清题中的规律是解本题的关键．
练习册系列答案
阶梯计算系列答案
相关题目
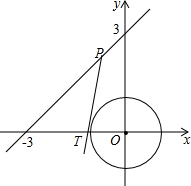如图，在直角坐标系中，圆O是以坐标原点为圆心，半径为1的圆，直线L的方程为x-y+3=0，在L上任取一点P作圆O的切线，切点为T，则PT长的最小值是$\frac{\sqrt{14}}{2}$．
3．若a＜b＜0，化简$\root{3}{{{{（{a-b}）}^3}}}-\sqrt{{{（{a-b}）}^2}}+\root{3}{a^3}-\sqrt{b^2}$的结果为（ ）
| A． | 3a-b | B． | 3（b-a） | C． | a-b | D． | b-a |