题目内容
9.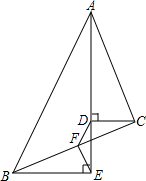 如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连结DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是$\sqrt{2}$.
如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连结DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是$\sqrt{2}$.
分析 延长CD交AB于M,延长AC、BE交于点N,作EH⊥DF交DF的延长线于H,先证明AN=AC,AB=AN,根据等腰三角形的性质得到DM=DC,EB=EN,根据三角形中位线定理求得DF=FE=2,在RT△EHF中求出HE即可解决问题.
解答  解:延长CD交AB于M,延长AC、BE交于点N,作EH⊥DF交DF的延长线于H.
解:延长CD交AB于M,延长AC、BE交于点N,作EH⊥DF交DF的延长线于H.
∵AD⊥CM,
∴∠ADC=∠ADM=90°,
∵∠DAM=∠DAC,∠DAM+∠AMC=90°,∠DAC+∠ACM=90°,
∴∠AMC=∠ACM,
∴AM=AC=6,同理可以证明:AB=AN=10,
∴BM=CN=4,
∵AD⊥CM,AM=AC,
∴DM=DC,同理BE=EN,
∵BF=CF,
∴FD=$\frac{1}{2}$BM=2,EF=$\frac{1}{2}$CN=2,
∵∠DFE=135°,
∴∠EFH=45°,EH=$\frac{\sqrt{2}}{2}$EF=$\sqrt{2}$,
∴S△DEF=$\frac{1}{2}$•DF•HE=$\sqrt{2}$,
故答案为$\sqrt{2}$.
点评 本题考查等腰三角形的性质、三角形中位线定理、直角三角形的有关知识,解题的关键是正确添加辅助线构造等腰三角形,利用三角形中位线定理解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.在平面直角坐标系中作△OMN,其中三个顶点分别是O(0,0),M(1,1),N(x,y)(-2≤x≤2,-2≤y≤2,x,y的值均为整数),则所作△OMN不是直角三角形的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{6}$ |
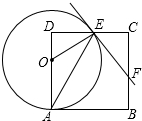 如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.
如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.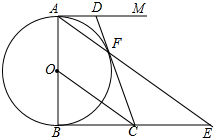 如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.
如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.