题目内容
2．已知一个六边形的每个内角为120°，其中连续四边的长依次为8、664、10、650，则此六边形的周长应是2006．分析 先延长并反向延长AB，CD，EF，构成一个等边三角形，再将这个六边形以外的多边形减去即可得这个六边形的周长．
解答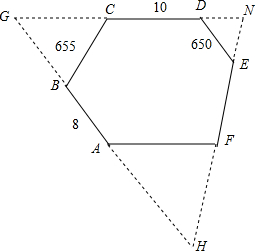 
解：如图，延长并反向延长AB，CD，EF．
∵六边形ABCDEF的每个内角都是120°，
∴∠G=∠H=∠N=60°，
∴△GHN是等边三角形，
∴六边形ABCDEF的周长=HN+AG+CD=（655+10+650）+（8+655）+10=2006．
答：该六边形周长是2006．
故答案为：2006．
点评 本题考查了等边三角形的判定与性质，解决本题的关键是构造等边三角形，根据等边三角形的三边相等的性质求解．
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
3．若a＜b＜0，化简$\root{3}{{{{（{a-b}）}^3}}}-\sqrt{{{（{a-b}）}^2}}+\root{3}{a^3}-\sqrt{b^2}$的结果为（ ）
| A． | 3a-b | B． | 3（b-a） | C． | a-b | D． | b-a |
4．下列二次根式是最简二次根式的是（ ）
| A． | $\sqrt{2a}$ | B． | $\sqrt{\frac{b}{3}}$ | C． | $\sqrt{{c}^{3}}$ | D． | $\sqrt{8{d}^{2}}$ |
14．在平面直角坐标系中作△OMN，其中三个顶点分别是O（0，0），M（1，1），N（x，y）（-2≤x≤2，-2≤y≤2，x，y的值均为整数），则所作△OMN不是直角三角形的概率为（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{5}{6}$ |
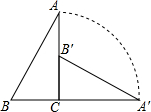如图，已知△ABC中∠A=30°，∠C=90°，AB=4，将△ABC绕点C顺时针旋转90°得到△A′B′C′．在整个旋转过程中．