题目内容
6.经过⊙O的直径AB的延长线上一个动点P作圆的切线,C为切点,∠APC的角平分线交AC于点E,∠PEC的大小会随着P的位置改变而改变吗?为什么?分析 如图连接OC,由∠CPO+∠COP=90°推出2∠APE+2∠A=90°由此即可证明.
解答 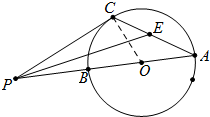 解:结论:∠PEC=45°不会随着P的位置改变而改变.
解:结论:∠PEC=45°不会随着P的位置改变而改变.
理由:如图连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵PC是⊙O切线,
∴OC⊥PC,
∴∠PCO=90°,
∴∠CPO+∠COP=90°,
∵∠APC=2∠APE,∠COP=∠A+∠OCA=2∠A,
∴2∠APE+2∠A=90°,
∴∠A+∠APE=45°,
∴∠PEC=∠APE+∠A=45°.
点评 本题考查切线的性质、等腰三角形的性质等知识,解题的关键是巧妙利用等式的性质,学会转化的思想,要求∠PEC只要求∠APE+∠A即可,属于中考常考题型.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
14.在平面直角坐标系中作△OMN,其中三个顶点分别是O(0,0),M(1,1),N(x,y)(-2≤x≤2,-2≤y≤2,x,y的值均为整数),则所作△OMN不是直角三角形的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{6}$ |
16.下列实数中,无理数是( )
| A. | $\sqrt{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{2}$ |
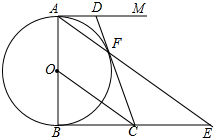 如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.
如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.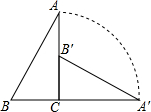 如图,已知△ABC中∠A=30°,∠C=90°,AB=4,将△ABC绕点C顺时针旋转90°得到△A′B′C′.在整个旋转过程中.
如图,已知△ABC中∠A=30°,∠C=90°,AB=4,将△ABC绕点C顺时针旋转90°得到△A′B′C′.在整个旋转过程中.