Question

18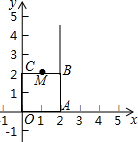．如图，正方形ABCO在平面直角坐标系中，点A、B、C坐标分别是A（2，0）、B（2，2）、C（0，2），点M是BC中点，点P（0，t）是线段OC上的一动点，射线PM交直线AB于点Q．
（1）点M的坐标为（1，2）；
（2）用含t的式子表示点Q坐标：（2，4-t）；
（3）若△APQ是等腰三角形，求点P的坐标．

Answer 1

分析 （1）M是BC的中点，则M的坐标是B和C的坐标的平均数，据此即可求得；
（2）利用待定系数法求得直线PM的解析式，然后求得与AB的交点即可；
（3）求得AP²，PQ²和AQ²，然后根据AP=AQ，AP=PQ和AQ=PQ三种情况，列方程求解．

解答 解：（1）M的坐标是（1，2）；
（2）设直线PM的解析式是y=kx+b，
则$\left\{\begin{array}{l}{b=t}\\{k+b=2}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{b=t}\\{k=2-t}\end{array}\right.$，
则直线PM的解析式是y=（2-t）x+t，
令x=2，则y=2（2-t）+t=4-t．
则Q的坐标是（2，4-t）；
（3）AP²=2²+t²=4+t²，
AQ²=（4-t）²，
PQ²=2²+（4-t-t）²=4+（4-2t）²，
当AP=AQ时，4+t²=（4-t）²时，t=$\frac{3}{2}$；
当AP=PQ时，4+t²=4+（4-2t）²，解得：t=$\frac{4}{3}$或4（舍去）；
当AQ=PQ时，4+（4-2t）²=（4-t）²，
解得：2或$\frac{1}{3}$．
总之，P的坐标是（0，$\frac{3}{2}$）或（0，$\frac{4}{3}$）（0，2）或（0，$\frac{1}{3}$）．

点评 本题考查了待定系数法求函数的解析式，以及等腰三角形的性质，正确利用t表示出AP、AQ和PQ的长是关键．