题目内容
3．用换元法解方程$\frac{5{（x}^{2}-x）}{{x}^{2}+1}$+$\frac{2{（x}^{2}+1）}{{x}^{2}-x}$=6．分析 根据换元法，可得分式方程，根据解分式方程，可得答案．
解答 解：设u=$\frac{{x}^{2}-x}{{x}^{2}+1}$，原方程等价于
5u+$\frac{2}{u}$=6．
5u2-6u+2=0．
∵△=（-6）2-4×5×2=36-40=-4＜0，
∴5u2-6u+2=0无实数根，
分式方程无解．
点评 本题考查了解分式方程，利用换元法是解题关键，又利用了根的判别式．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
14．y轴正半轴上距原点2个单位长度的点的坐标为（ ）
| A． | （2，0） | B． | （-2，0） | C． | （0，2） | D． | （0，-2） |
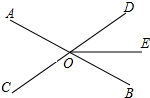如图，直线AB、CD相交于点O，OE平分∠BOD，若∠AOD=2∠DOB，则∠EOB=30°．
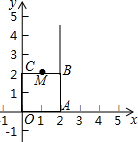如图，正方形ABCO在平面直角坐标系中，点A、B、C坐标分别是A（2，0）、B（2，2）、C（0，2），点M是BC中点，点P（0，t）是线段OC上的一动点，射线PM交直线AB于点Q．