题目内容
16.如图,⊙O为Rt△ACB的外接圆,点P是AB延长线上的一点,PC切⊙O于点C,连接AC.(1)若AC=CP,求$\frac{AC}{AP}$的值.
(2)若sin∠APC=$\frac{7}{25}$,求tan∠ABC.
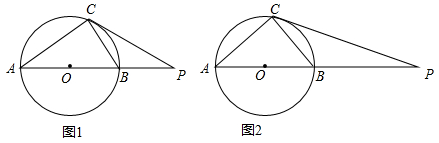
分析 (1)连接OC,根据等腰三角形的性质得到∠A=∠P,根据切线的性质得到∠OCP=90°,求出∠P=30°,于是得到$\frac{OC}{PC}$$\frac{\sqrt{3}}{3}$,根据相似三角形的性质即可得到结论;
(2)如图2,连接OC,根据sin∠APC=$\frac{OC}{OP}$=$\frac{7}{25}$,设OC=7k,OP=25k,求出AP=32k,PC=$\sqrt{O{P}^{2}-O{C}^{2}}$=24k,根据相似三角形的性质即可得到结论.
解答 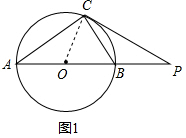 解:(1)连接OC,
解:(1)连接OC,
∵AC=PC,
∴∠A=∠P,
∵PC切⊙O于点C,
∴∠OCP=90°,
∵∠COP=∠A+∠ACO,
∵OA=OC,
∴∠A=∠ACO,
∴∠COP=2∠A=2∠P,
∴∠P+∠COP=90°,
∴∠P=30°,
∴$\frac{OC}{PC}$$\frac{\sqrt{3}}{3}$,
∵∠A=∠A,∠ACO=∠P,
∴△AOC∽△APC,
∴$\frac{AC}{AP}=\frac{OC}{CP}$=$\frac{\sqrt{3}}{3}$;
(2)如图2,连接OC,
∵PC切⊙O于点C,
∴OC⊥PC,∠A=∠BCP,
∵sin∠APC=$\frac{OC}{OP}$=$\frac{7}{25}$,
∴设OC=7k,OP=25k,
∴AP=32k,PC=$\sqrt{O{P}^{2}-O{C}^{2}}$=24k,
∵∠P=∠P,
∴△ACP∽△CBP,
∴$\frac{BC}{AC}=\frac{PC}{PA}$=$\frac{24k}{32k}$=$\frac{3}{4}$,
∵∠ACB=90°,
∴tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$.
点评 本题考查了相似三角形的判定和性质,切线的性质,勾股定理,等腰三角形的性质,正确的作出辅助线是解题的关键.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案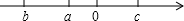 有理数a、b在数轴上的位置如图,则|a-b|-2|a-c|-|b+c|=( )
有理数a、b在数轴上的位置如图,则|a-b|-2|a-c|-|b+c|=( )| A. | a+c | B. | a-c | C. | 2a-2b | D. | 3a-c |
| A. | 2cm,2cm,3cm | B. | 1cm,2cm,3cm | C. | 2cm,3cm,6cm | D. | 5cm,15cm,8cm |
 如图,在?ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AG⊥BC,EF=$\sqrt{3}$,求AG的长.
如图,在?ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AG⊥BC,EF=$\sqrt{3}$,求AG的长. 如图,在矩形ABCD中,AB=6cm,BD=10cm
如图,在矩形ABCD中,AB=6cm,BD=10cm