题目内容
1.已知a是$\sqrt{17}$-3的整数部分,b是$\sqrt{17}$-3的小数部分,那么(-a)3+(b+4)2的平方根是( )| A. | 4 | B. | ±2 | C. | ±8 | D. | ±4 |
分析 根据4<$\sqrt{17}$<5,利用不等式的性质可得1<$\sqrt{17}$-3<2,求出a、b 的值,再代入(-a)3+(b+4)2计算,根据平方根的定义求解.
解答 解:∵4<$\sqrt{17}$<5,
∴1<$\sqrt{17}$-3<2,
∴a=1,b=$\sqrt{17}$-4,
∴(-a)3+(b+4)2=(-1)3+($\sqrt{17}$-4+4)2=-1+17=16,
∴(-a)3+(b+4)2的平方根是±$\sqrt{16}$=±4.
故选D.
点评 此题主要考查了估算无理数的大小,正确得出a,b的值是解题关键.

练习册系列答案
相关题目
12.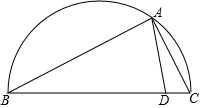 如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )
如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )
 如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )
如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )| A. | $\frac{9}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{6}{5}$ |
6.在0,-2,-1,$\frac{1}{2}$这四个数中,最小的数是( )
| A. | 0 | B. | -2 | C. | -1 | D. | $\frac{1}{2}$ |
13.下列运算正确的是( )
| A. | x3+x3=2x6 | B. | (x2)3=x5 | C. | x6÷x2=x3 | D. | x2•x3=x5 |
10.已知点P(a,2),Q(-1,b)关于x轴对称,则点(a,b)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |