题目内容
6.在平面直角坐标系中,已知点A(a,$\sqrt{3}$),点P在x轴上,若使得△AOP是等腰三角形的点P恰好有2个,则满足条件的a值可能是±1.分析 分两种情况进行讨论:①点A在第一象限,②点A在第二象限,分别根据△AOP是等腰三角形进行计算求解.
解答 解:如图所示,当点P恰好有2个时,分两种情况:
①若点A在第一象限,过点A作AH⊥x轴于H,则∠AOH=60°,
∵点A的纵坐标为$\sqrt{3}$,
∴AH=$\sqrt{3}$,
∴Rt△AOH中,OH=$\frac{AH}{tan60°}$=1,
∴a=1;
②当点A在第二象限时,同理可得a=-1.
故答案为:±1.
点评 本题主要考查了等腰三角形的判定与性质以及解直角三角形的运用,解决问题的关键是画出图形,根据AO与x轴的夹角为60°进行判断.

练习册系列答案
相关题目
17.下列化简正确的是( )
| A. | 2a+3b=5ab | B. | 7ab-3ab=4 | C. | 2ab+3ab=5ab | D. | a2+a2=a4 |
14.在Rt△ABC中,∠C=90°,AB=6,cosB=$\frac{2}{3}$,则BC的长为( )
| A. | $\sqrt{5}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 5 |
11.若方程组$\left\{\begin{array}{l}{x+y=a}\\{x-y=4a}\end{array}\right.$的解是二元一次方程3x-5y-90=0的一个解,则a的值是( )
| A. | 3 | B. | 2 | C. | 6 | D. | 7 |
15.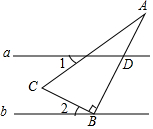 直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )
直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )
 直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )
直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |