题目内容
3.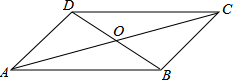 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )| A. | AB∥DC,AD∥BC | B. | AB∥DC,∠A=∠C | C. | AO=BO,CO=DO | D. | ∠A=∠C,∠B=∠D |
分析 利用平行四边形的判定定理分别进行分析即可.
解答 解:A、AB∥DC,AD∥BC根据两组对边分别平行的四边形是平行四边形判定四边形ABCD是平行四边形,故此选项不合题意;
B、由AB∥DC,∠A=∠C可证明∠B=∠D,然后可根据两组对角分别相等的四边形是平行四边形判定四边形ABCD是平行四边形,故此选项不合题意;
C、AO=BO,CO=DO不能判定四边形ABCD是平行四边形,故此选项符合题意;
D、∠A=∠C,∠B=∠D然后可根据两组对角分别相等的四边形是平行四边形判定四边形ABCD是平行四边形,故此选项不合题意;
故选:C.
点评 此题主要考查了平行四边形的判定定理,关键是掌握两组对边分别平行的四边形是平行四边形.两组对边分别相等的四边形是平行四边形.一组对边平行且相等的四边形是平行四边形.两组对角分别相等的四边形是平行四边形.对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目
11.如果$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax+by=0}\\{bx-cy=1}\end{array}\right.$的解,那么,下列各式中成立的是( )
| A. | a+4c=2 | B. | 4a+c=2 | C. | a+4c+2=0 | D. | 4a+c+2=0 |
15.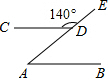 如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
 如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
如图,AB∥CD,∠CDE=140°,则∠A的度数为( )| A. | 70° | B. | 65° | C. | 50° | D. | 40° |
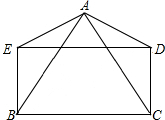 如图,?BCDE中,EA⊥AC于A,BA⊥AD于A,求证:四边形BCDE是矩形.
如图,?BCDE中,EA⊥AC于A,BA⊥AD于A,求证:四边形BCDE是矩形.