题目内容
12．定义：直线l1与l2相交于点O，对于平面内任意一点P1点P到直线l1与l2的距离分别为p、q则称有序实数对（p，q）是点P的“距离坐标”．根据上述定义，“距离坐标”是（3，2）的点的个数有4个．分析 首先根据“距离坐标”的含义，可得“距离坐标”是（3，2）到直线l1与l2的距离分别为3、2，然后根据到直线l1的距离是3的点在与直线l1平行且与l1的距离是3的两条平行线上，到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线上，一共有4个交点，所以“距离坐标”是（3，2）的点的个数有4个，据此解答即可．
解答 解：“距离坐标”是（3，2）到直线l1与l2的距离分别为3、2，
因为到直线l1的距离是3的点在与直线l1平行且与l1的距离是3的两条平行线上，
到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线上，一共有4个交点，
所以“距离坐标”是（3，2）的点的个数有4个．
故答案为：4．
点评 此题主要考查了点的“距离坐标”的含义以及应用，考查了分析推理能力，考查了分类讨论思想的应用，要熟练掌握，解答此题的关键是要明确：“距离坐标”是（3，2）到直线l1与l2的距离分别为3、2．
练习册系列答案
阅读快车系列答案
相关题目
3．
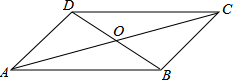如图，四边形ABCD的对角线AC、BD相交于点O，则下列条件不能判定四边形ABCD是平行四边形的是（ ）
如图，四边形ABCD的对角线AC、BD相交于点O，则下列条件不能判定四边形ABCD是平行四边形的是（ ）| A． | AB∥DC，AD∥BC | B． | AB∥DC，∠A=∠C | C． | AO=BO，CO=DO | D． | ∠A=∠C，∠B=∠D |
20．
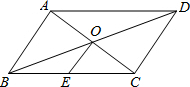如图，平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（ ）
如图，平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（ ）| A． | 3cm | B． | 6cm | C． | 9cm | D． | 12cm |
7．在同一平面内，有三条直线a、b、c，下列说法：
①若a与b相交，b与c相交，则a与c相交；
②若a∥b，b与c相交（不重合），则a与c相交；
③若a⊥b，b⊥c，则a⊥c，
④若a∥b，b∥c，则a∥c，
其中正确的结论的个数为（ ）
①若a与b相交，b与c相交，则a与c相交；
②若a∥b，b与c相交（不重合），则a与c相交；
③若a⊥b，b⊥c，则a⊥c，
④若a∥b，b∥c，则a∥c，
其中正确的结论的个数为（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
17．实数-2，0.3，$\frac{1}{7}$，$\sqrt{2}$，-π中，无理数的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，三角形ABC在直角坐标系中，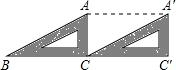
如图，将三角尺ABC沿BC方向平移，得到三角形A′CC′．已知∠B=30°，∠ACB=90°，则∠BAA′的度数为150°．