题目内容
14.(1)$\sqrt{32}$-2(5$\sqrt{2}$-$\sqrt{18}$);(2)$\sqrt{48}$-$\sqrt{54}$÷$\sqrt{2}$+(3-$\sqrt{3}$)(3+$\sqrt{3}$).
分析 (1)直接利用二次根式的性质化简进而合并同类二次根式求出即可;
(2)直接利用二次根式的性质化简进而合并同类二次根式求出即可.
解答 解:(1)原式=4$\sqrt{2}$-2(5$\sqrt{2}$-3$\sqrt{2}$)
=4$\sqrt{2}$-4$\sqrt{2}$
=0;
(2)原式=4$\sqrt{3}$-$\sqrt{27}$+32-($\sqrt{3}$)2
=4$\sqrt{3}$-3$\sqrt{3}$+9-3
=$\sqrt{3}$+6.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
5.如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第5个图案需要的棋子数为( )


| A. | 61 | B. | 91 | C. | 152 | D. | 169 |
19.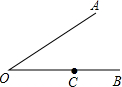 如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )
如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )
 如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )
如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 不能确定 |
3.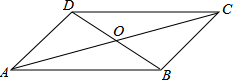 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )| A. | AB∥DC,AD∥BC | B. | AB∥DC,∠A=∠C | C. | AO=BO,CO=DO | D. | ∠A=∠C,∠B=∠D |

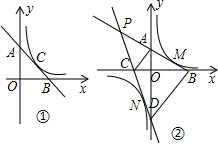
 如图,三角形ABC在直角坐标系中,
如图,三角形ABC在直角坐标系中,