题目内容
8.先化简,再求值:$\frac{4{a}^{3}-a{b}^{2}}{4{a}^{3}-4{a}^{2}b+a{b}^{2}}$,其中a=0.5,b=2.分析 首先把分式的分子分母分解因式,然后约分化简,再代入a、b的值计算即可.
解答 解:原式=$\frac{a(2a+b)(2a-b)}{a(4{a}^{2}-4ab+{b}^{2})}$=$\frac{a(2a+b)(2a-b)}{a(2a-b)^{2}}$=$\frac{2a+b}{2a-b}$,
当a=0.5,b=2时,原式=$\frac{2×0.5+2}{2×0.5-2}$=$\frac{3}{-1}$=-3.
点评 此题主要考查了分式的化简求值,关键是正确把分子分母分解因式,找到公因式,进行约分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.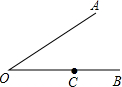 如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )
如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )
 如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )
如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 不能确定 |
3.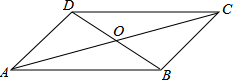 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )| A. | AB∥DC,AD∥BC | B. | AB∥DC,∠A=∠C | C. | AO=BO,CO=DO | D. | ∠A=∠C,∠B=∠D |
20.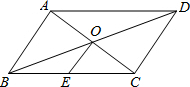 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
17.实数-2,0.3,$\frac{1}{7}$,$\sqrt{2}$,-π中,无理数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于O点,求证:BE=CD.
如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于O点,求证:BE=CD.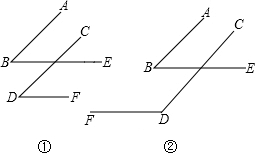
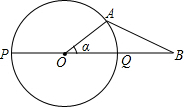 如图,PQ为⊙O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在⊙O的上半圆运动(含P、Q两点),连结AB,设∠AOB=α.有以下结论:
如图,PQ为⊙O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在⊙O的上半圆运动(含P、Q两点),连结AB,设∠AOB=α.有以下结论: