题目内容
13.在图中,A(-1,4)、B(-4,-1)、C(1,1),将△ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题.(1)平移后的三个顶点坐标分别为:A1(4,7),B1(1,2),C1(6,4);
(2)画出平移后△A1B1C;
(3)求△ABC的面积;
(4)若点D在过点B1且平行于x轴的直线上,若△A1B1D的面积等于△ABC的面积,请直接写出所有满足条件点D的坐标.
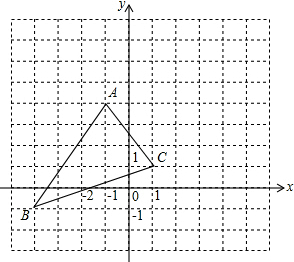
分析 (1)根据横坐标右移加,左移减,纵坐标上移加,下移减即可得出三个顶点的坐标;
(2)根据网格结构分别找到三个顶点的位置,再顺次连接即可得出答案;
(3)将△ABC补全为矩形,然后利用作差法求解即可;
(4)设点D的坐标为(x,2),根据△A1B1D的面积等于△ABC的面积,列出方程$\frac{1}{2}$|x-1|×5=$\frac{19}{2}$,解方程即可.
解答 解:(1)∵A(-1,4)、B(-4,-1)、C(1,1),将△ABC向右平移5个单位长度,再向上平移3个单位长度,
∴A1坐标为(4,7),点B1坐标为(1,2),C1坐标为(6,4);
(2)所画图形如下: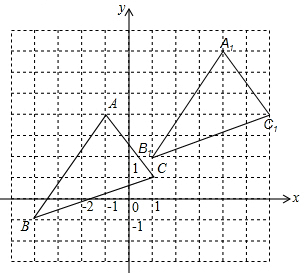
(3)如图,
S△ABC=S矩形EBGF-S△ABE-S△GBC-S△AFC
=5×5-$\frac{1}{2}$×5×3-$\frac{1}{2}$×5×2-$\frac{1}{2}$×2×3
=25-$\frac{15}{2}$-5-3
=$\frac{19}{2}$;
(4)设点D的坐标为(x,2),
∵△A1B1D的面积等于△ABC的面积,
∴$\frac{1}{2}$|x-1|×5=$\frac{19}{2}$,
解得x=$\frac{24}{5}$或-$\frac{14}{5}$.
∴点D的坐标为($\frac{24}{5}$,2)或(-$\frac{14}{5}$,2).
故答案为(4,7),(1,2),(6,4).
点评 本题考查了作图-平移变换,平移的性质,三角形的面积.解答本题的关键是根据平移的特点准确作出图形.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
5.如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第5个图案需要的棋子数为( )


| A. | 61 | B. | 91 | C. | 152 | D. | 169 |
3.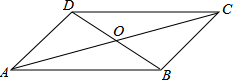 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )| A. | AB∥DC,AD∥BC | B. | AB∥DC,∠A=∠C | C. | AO=BO,CO=DO | D. | ∠A=∠C,∠B=∠D |


 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.
 如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于O点,求证:BE=CD.
如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于O点,求证:BE=CD.