题目内容

15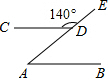．如图，AB∥CD，∠CDE=140°，则∠A的度数为（　　）
A．70°B．65°C．50°D．40°

分析 由邻补角的定义，可求得∠ADC的度数，又由AB∥CD，根据两直线平行，内错角相等，即可求得答案．

解答 解：∵∠CDE=140°，
∴∠CDA=180°-∠CDE=40°，
∵AB∥CD，
∴∠A=∠ADC=40°．
故选D．

点评 此题考查了平行线的性质．注意两直线平行，内错角相等定理的应用是解此题的关键．

练习册系列答案
相关题目
5．如图，是用棋子摆成的图案，摆第1个图案需要7枚棋子，摆第2个图案需要19枚棋子，摆第3个图案需要37枚棋子，按照这样的方式摆下去，则摆第5个图案需要的棋子数为（　　）
A．61B．91C．152D．169
6．（1）如图①，一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴分别交于点A、B，与反比例函数y=$\frac{m}{x}$的图象只有一个公共点C，求m的值及AC、CB的长；
（2）如图②，直线PAB分别交x轴、y轴于点B、A，直线PCD分别交x轴、y轴于点C、D，且分别与反比例函数y=$\frac{m}{x}$的图象都只有一个公共点M、N．
①求证：AM=MB，CN=ND；
②求证：AC∥BD．
3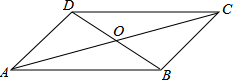．如图，四边形ABCD的对角线AC、BD相交于点O，则下列条件不能判定四边形ABCD是平行四边形的是（　　）
A．AB∥DC，AD∥BCB．AB∥DC，∠A=∠CC．AO=BO，CO=DOD．∠A=∠C，∠B=∠D
10．如图，在?ABCD中，DB=DC，∠C=72°，AE⊥BD于E，求∠DAE的度数．
20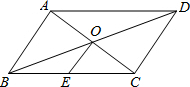．如图，平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（　　）
A．3cmB．6cmC．9cmD．12cm
7．在同一平面内，有三条直线a、b、c，下列说法：
①若a与b相交，b与c相交，则a与c相交；
②若a∥b，b与c相交（不重合），则a与c相交；
③若a⊥b，b⊥c，则a⊥c，
④若a∥b，b∥c，则a∥c，
其中正确的结论的个数为（　　）
A．1个B．2个C．3个D．4个
4． 如图，三角形ABC在直角坐标系中，
（1）若把三角形ABC向上平移2个单位，再向左平移1个单位得到三角形A′B′C′，请写出A′，B′，C′的坐标．
（2）求出三角形ABC的面积．
9．在△ABC中，∠BAC=90°，AB＜AC，M是BC边的中点，MN⊥BC交AC于点N．动点P从点B出发，沿射线BA以每秒$\sqrt{3}$个长度单位运动，连接MP，同时动点Q从点N出发，沿射线NC以一定的速度运动，且始终保持MQ⊥MP，设运动时间为t秒（t＞0）．
（1）求证：△BMP∽△NMQ；
（2）若∠B=60°，AB=4$\sqrt{3}$，设△APQ的面积为S，求S与t的函数关系式；
（3）当BP=$\sqrt{3}$，PQ=$2\sqrt{13}$时，求CQ的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网