题目内容
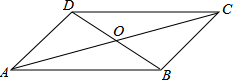
13.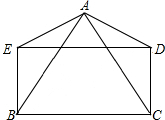 如图,?BCDE中,EA⊥AC于A,BA⊥AD于A,求证:四边形BCDE是矩形.
如图,?BCDE中,EA⊥AC于A,BA⊥AD于A,求证:四边形BCDE是矩形.
分析 连接BD,CE,相交于点O,再连接AO,根据EA⊥AC,BA⊥AD,可得出OA=$\frac{1}{2}$BD=$\frac{1}{2}$CE,从而得出BD=CE,根据对角线相等的平行四边形为矩形即可证明四边形BCDE是矩形.
解答 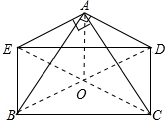 证明:连接BD,CE,相交于点O,再连接AO,
证明:连接BD,CE,相交于点O,再连接AO,
∵EA⊥AC,BA⊥AD,
∴∠CAE=∠BAD=90°,
∴OA=$\frac{1}{2}$BD=$\frac{1}{2}$CE,
∵四边形BCDE为平行四边形,
∴OB=OD,OC=OE,
∴BD=CE,
∴四边形BCDE是矩形(对角线相等的平行四边形是矩形).
点评 本题考查了矩形的判定,直角三角形的性质的应用,主要考查学生运用定理进行推理的能力,注意:对角线相等的平行四边形是矩形.

练习册系列答案
相关题目
3. 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )| A. | AB∥DC,AD∥BC | B. | AB∥DC,∠A=∠C | C. | AO=BO,CO=DO | D. | ∠A=∠C,∠B=∠D |
 如图,三角形ABC在直角坐标系中,
如图,三角形ABC在直角坐标系中,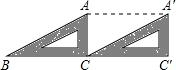 如图,将三角尺ABC沿BC方向平移,得到三角形A′CC′.已知∠B=30°,∠ACB=90°,则∠BAA′的度数为150°.
如图,将三角尺ABC沿BC方向平移,得到三角形A′CC′.已知∠B=30°,∠ACB=90°,则∠BAA′的度数为150°.