题目内容
11.如果$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax+by=0}\\{bx-cy=1}\end{array}\right.$的解,那么,下列各式中成立的是( )| A. | a+4c=2 | B. | 4a+c=2 | C. | a+4c+2=0 | D. | 4a+c+2=0 |
分析 把$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{ax+by=0}\\{bx-cy=1}\end{array}\right.$可得:$\left\{\begin{array}{l}{-a+2b=0①}\\{-b-2c=1②}\end{array}\right.$,然后②×2+①可得:-a-4c=2,再整理可得答案.
解答 解:把$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{ax+by=0}\\{bx-cy=1}\end{array}\right.$可得:$\left\{\begin{array}{l}{-a+2b=0①}\\{-b-2c=1②}\end{array}\right.$,
②×2得:-2b-4c=2③,
①+③得:-a-4c=2,
a+4c+2=0,
故选:C.
点评 此题主要考查了二元一次方程组的解,关键是掌握二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.

练习册系列答案
相关题目
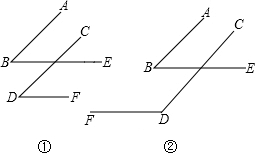
19.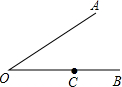 如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )
如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )
 如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )
如图,过∠AOB边OB上一点C作OA的平行线,以C为顶点的角与∠AOB的关系是( )| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 不能确定 |
3.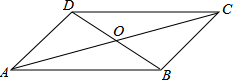 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )| A. | AB∥DC,AD∥BC | B. | AB∥DC,∠A=∠C | C. | AO=BO,CO=DO | D. | ∠A=∠C,∠B=∠D |
20.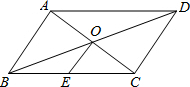 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.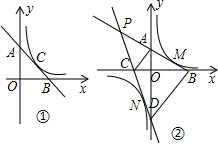
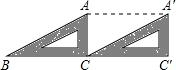 如图,将三角尺ABC沿BC方向平移,得到三角形A′CC′.已知∠B=30°,∠ACB=90°,则∠BAA′的度数为150°.
如图,将三角尺ABC沿BC方向平移,得到三角形A′CC′.已知∠B=30°,∠ACB=90°,则∠BAA′的度数为150°.