Question

10．（1）已知：如图1，点E、F分别为平行四边形ABCD的BC、AD边上的点，且∠1=∠2，求证；AE=FC；
（2）如图2所示，已知点O为正方形ABCD对角线AC上一点，以点O为圆心，一OA长为半径的⊙O与BC相切于点MM，与AD，AD分别相交于点E、F，求证：CD与⊙O相切．

Answer 1

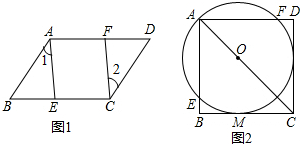
分析 （1）只要证明AE∥CF即可证明四边形AECF是平行四边形，由此解决问题．
（2）如图2中，连接OM，作ON⊥CD于N，只要证明ON等于半径即可解决问题．

解答 解：（1）如图1中，

∵四边形ABCD是平行四边形，
∴∠BAD=∠BCD，AD∥BC，
∵∠1=∠2，
∴∠DAE=∠BCF，∠DFC=∠BCF，
∴∠DFC=∠DAE，
∴AE∥CF，
∵AF∥EC，
∴四边形AECF是平行四边形，
∴AE=CF．

（2）如图2中，连接OM，作ON⊥CD于N．

∵四边形ABCD是正方形，
∴AC平分∠BCD，
∵M是切点，
∴OM⊥BC，∵ON⊥CD，
∴OM=ON，
∴CD是⊙O的切线．

点评 本题考查平行四边形的性质、正方形的性质、切线的判定和性质等知识，解题的关键是灵活应用这些知识解决问题，属于中考常考题型．