题目内容
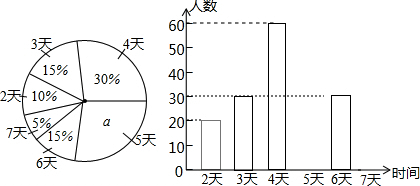
6.某市教育行政部门为了了解七年级学生每学期参加综合实践活动的情况,随机抽样调查了实验中学七年级学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,回答下列问题:(1)填空:扇形统计图中a=25%,该校七年级学生总人数为200人;
(2)根据图中信息,补全条形统计图;
(3)填空:扇形统计图中,“活动时间为4天”的扇形的圆心角的度数为108°;
(4)如果该市共有七年级学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
分析 (1)用1减去已知的各个百分比,求得a的值,再用人数除以相应的百分比,求得该校七年级学生总人数;
(2)先根据百分比乘上总人数,求得“活动时间为5天”和“活动时间为7天”的人数,再进行画图;
(3)根据统计图,用“活动时间为4天”的百分比乘上360°,求得扇形的圆心角的度数;
(4)根据“活动时间不少于4天”的百分比之和,乘上该市七年级学生总数,求得该市“活动时间不少于4天”的七年级学生数.
解答 解:(1)a=1-10%-15%-30%-15%-5%=25%,该校七年级学生总人数=20÷10%=200(人),
故答案为:25%,200;
(2)“活动时间为5天”的人数为:25%×200=50(人),
“活动时间为7天”的人数为:5%×200=10(人),
条形统计图如下: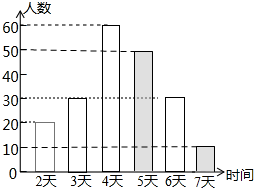
(3)“活动时间为4天”的扇形的圆心角的度数=30%×360°=108°,
故答案为:108°;
(4)(30%+25%+15%+5%)×6000=4500,
故“活动时间不少于4天”的大约有4500人.
点评 本题主要考查了扇形统计图与条形统计图,计算时注意,各部分扇形圆心角的度数=部分占总体的百分比×360°.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
16. 某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
 某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )| A. | 在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球” | |
| B. | 从一副扑克牌中任意抽取一张,这张牌是“红色的” | |
| C. | 掷一枚质地均匀的硬币,落地时结果是“正面朝上” | |
| D. | 只一个质地均匀的正六面体骰子,落地时面朝上的点数是6 |
5.若$\frac{{a}^{-1}+b}{a+{b}^{-1}}$=k,则$\frac{{a}^{-2}+{b}^{2}}{{a}^{2}+{b}^{-2}}$=( )
| A. | k | B. | $\frac{1}{2}$k | C. | k2 | D. | $\frac{1}{2}$k2 |
12.抛物线y=x2+bx+c与x轴只有一个公共点,且过点A(m+1,n),B(m-9,n),则n=( )
| A. | 16 | B. | 18 | C. | 20 | D. | 25 |