题目内容
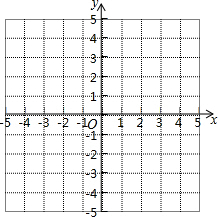 已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题:
已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题:(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积;
(2)在平面直角坐标系中画出△A′B′C′,使它与△ABC关于x轴对称,并写出△A′B′C′三顶点的坐标;
(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△A′B′C′内部的对应点M′的坐标.
考点:作图-轴对称变换
专题:
分析:(1)根据点的坐标,直接描点,根据点的坐标可知,AB∥x轴,且AB=3-(-2)=5,点C到线段AB的距离3-1=2,根据三角形面积公式求解;
(2)分别作出点A、B、C关于x轴对称的点A'、B'、C',然后顺次连接A′B′、B′C′、A′C′,并写出三个顶点坐标;
(3)根据两三角形关于x轴对称,写出点M'的坐标.
(2)分别作出点A、B、C关于x轴对称的点A'、B'、C',然后顺次连接A′B′、B′C′、A′C′,并写出三个顶点坐标;
(3)根据两三角形关于x轴对称,写出点M'的坐标.
解答: 解:(1)描点如图,
解:(1)描点如图,
由题意得,AB∥x轴,且AB=3-(-2)=5,
∴S△ABC=
×5×2=5;
(2)如图;
A′(-2,-1)、B′(3,-1)、C′(2,-3);
(3)M'(x,-y).
 解:(1)描点如图,
解:(1)描点如图,由题意得,AB∥x轴,且AB=3-(-2)=5,
∴S△ABC=
| 1 |
| 2 |
(2)如图;
A′(-2,-1)、B′(3,-1)、C′(2,-3);
(3)M'(x,-y).
点评:本题考查了根据轴对称作图以及点的坐标的表示方法,能根据点的坐标表示三角形的底和高并求三角形的面积.
作轴对称后的图形的依据是轴对称的性质,基本作法是:
①先确定图形的关键点;
②利用轴对称性质作出关键点的对称点;
③按原图形中的方式顺次连接对称点.
作轴对称后的图形的依据是轴对称的性质,基本作法是:
①先确定图形的关键点;
②利用轴对称性质作出关键点的对称点;
③按原图形中的方式顺次连接对称点.

练习册系列答案
相关题目
 如图,已知△ABC,AC=BC=6,∠C=90°,O是AB的中点,⊙O与AC相切于点D,与BC相切于点E,设⊙O交OB于F,连DF并延长交CB的延长线于G.
如图,已知△ABC,AC=BC=6,∠C=90°,O是AB的中点,⊙O与AC相切于点D,与BC相切于点E,设⊙O交OB于F,连DF并延长交CB的延长线于G.
 如图,直线AB与x轴交于点A(2,0),与y轴交于B点,并且△AOB的面积为3.
如图,直线AB与x轴交于点A(2,0),与y轴交于B点,并且△AOB的面积为3. 如图,圆内接四边形ABDC中,DA平分∠BDC,
如图,圆内接四边形ABDC中,DA平分∠BDC,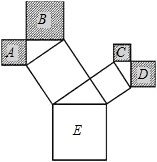 如图是勾股树的一部分,在一个正方形上以正方形的边为边长,构造直角三角形,再以直角边为边长作正方形,不断重复同个过程.设图中最大的正方形边长为5,正方形A,B,C,D,E的面积和为S,求S的值.
如图是勾股树的一部分,在一个正方形上以正方形的边为边长,构造直角三角形,再以直角边为边长作正方形,不断重复同个过程.设图中最大的正方形边长为5,正方形A,B,C,D,E的面积和为S,求S的值.