题目内容
 如图,已知△ABC,AC=BC=6,∠C=90°,O是AB的中点,⊙O与AC相切于点D,与BC相切于点E,设⊙O交OB于F,连DF并延长交CB的延长线于G.
如图,已知△ABC,AC=BC=6,∠C=90°,O是AB的中点,⊙O与AC相切于点D,与BC相切于点E,设⊙O交OB于F,连DF并延长交CB的延长线于G.(1)求∠ADG的度数;
(2)求由DG、GE和
 |
| ED |
考点:切线的性质,扇形面积的计算
专题:
分析:(1)连接OD,由AC为圆O的切线,根据切线的性质得到OD与AC垂直,又AC=BC,且∠C=90°,得到三角形ABC为等腰直角三角形,得到∠A=45°,所以∠CDG的度数,进而求出∠ADG的度数;
(2)阴影部分的面积=直角三角形CDG的面积-(正方形的面积-扇形ODE的面积).根据等腰直角三角形的性质可求出有关边AB、OD的长,以及圆心角∠DOE的度数.进而可根据扇形的面积和直角三角形的面积求得阴影部分的面积.
(2)阴影部分的面积=直角三角形CDG的面积-(正方形的面积-扇形ODE的面积).根据等腰直角三角形的性质可求出有关边AB、OD的长,以及圆心角∠DOE的度数.进而可根据扇形的面积和直角三角形的面积求得阴影部分的面积.
解答:解:(1)连接OD.
∵CD切⊙O于点D,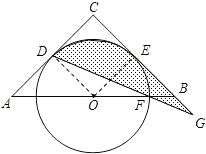
∴∠ODA=90°,∠DOA=45°,
∵OD=OF,
∴∠ODF=∠OFD=
∠DOA=22.5°,
∴∠CDG=∠CDO-∠ODF=90°-22.5°=67.5°,
∴∠ADG=180°-∠CDG=112.5°;
(2)连OE,
∵⊙O与AC相切于点D、与BC相切于点E,
∴DC=CE,OD⊥AC,OE⊥BC,
∵∠C=90°,
∴四边形ODCE为正方形,
∵AO=BO=
AB=
=3
,
∴OD=
BC=
×6=3,
∵∠BFG=∠BGF,
∴BG=BF=OB-OF=3
-3;
从而CG=CB+BG=3+3
;
∴S阴影=S△DCG-S正方形ODCE+S扇形ODE
=S△DCG-(S正方形ODCE-S扇形ODE)
=
×3×(3+3
)-(32-
π•32)
=
+
-
.
∵CD切⊙O于点D,

∴∠ODA=90°,∠DOA=45°,
∵OD=OF,
∴∠ODF=∠OFD=
| 1 |
| 2 |
∴∠CDG=∠CDO-∠ODF=90°-22.5°=67.5°,
∴∠ADG=180°-∠CDG=112.5°;
(2)连OE,
∵⊙O与AC相切于点D、与BC相切于点E,
∴DC=CE,OD⊥AC,OE⊥BC,
∵∠C=90°,
∴四边形ODCE为正方形,
∵AO=BO=
| 1 |
| 2 |
| 1 |
| 2 |
| AC2+BC2 |
| 2 |
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BFG=∠BGF,
∴BG=BF=OB-OF=3
| 2 |
从而CG=CB+BG=3+3
| 2 |
∴S阴影=S△DCG-S正方形ODCE+S扇形ODE
=S△DCG-(S正方形ODCE-S扇形ODE)
=
| 1 |
| 2 |
| 2 |
| 1 |
| 4 |
=
| 9π |
| 4 |
9
| ||
| 2 |
| 9 |
| 2 |
点评:此题考查了切圆的综合知识.在运用切线的性质时,若已知切点,连接切点和圆心,得垂直;若不知切点,则过圆心向切线作垂直,即“知切点连半径,无切点作垂直”.圆与相似三角形,及三角函数相融合的解答题、与切线有关的性质与判定有关的证明题是近几年中考的热点,故要求学生把所学知识融汇贯穿,灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=15°,则∠2的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=15°,则∠2的度数是( )| A、30° | B、25° |
| C、35° | D、20° |
 如图是由四个正方体摆成的立体图形,那么从上面看到的平面图形是( )
如图是由四个正方体摆成的立体图形,那么从上面看到的平面图形是( )A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,AD⊥BC于点D,E、F、G分别是BC、AC、AB的中点,若AB=
如图,在△ABC中,AD⊥BC于点D,E、F、G分别是BC、AC、AB的中点,若AB= 已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题:
已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题: