题目内容
如果关于x的方程
-
=x-
的解大于1,且不大于5,求m的整数值.
| x |
| 6 |
| 6m+1 |
| 3 |
| 5m-1 |
| 2 |
考点:一元一次不等式组的整数解,一元一次方程的解
专题:
分析:首先解方程,利用m表示出x的值,然后根据方程的解大于1,且不大于5即可得到一个关于m的不等式组,求得m的范围,进而确定m的整数值.
解答:解:解方程
-
=x-5m-
,
即
-2m-
=x-5m-
,
移项,得:
-x=6m-5m-
+
,
合并同类项,得:-
x=m-
,
系数化成1得:x=5-
m.
根据题意得:
,
解①得:m<
,
解②得:m≥0,
则不等式组的解集是:0≤m<
.
则m的整数值是:0,1,2,3.
| x |
| 6 |
| 6m+1 |
| 3 |
| 1 |
| 2 |
即
| x |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
移项,得:
| x |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
合并同类项,得:-
| 5 |
| 6 |
| 1 |
| 6 |
系数化成1得:x=5-
| 6 |
| 5 |
根据题意得:
|
解①得:m<
| 10 |
| 3 |
解②得:m≥0,
则不等式组的解集是:0≤m<
| 10 |
| 3 |
则m的整数值是:0,1,2,3.
点评:本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
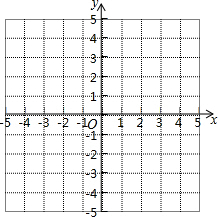 已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题:
已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题: 如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB、BC于点G、H.
如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB、BC于点G、H. 如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上),为了测量B、C两地之间的距离,某工程队乘坐热气球从C地出发垂直上升100m到达A处,在A处观察B地的仰角为30°,则BC两地间的距离为
如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上),为了测量B、C两地之间的距离,某工程队乘坐热气球从C地出发垂直上升100m到达A处,在A处观察B地的仰角为30°,则BC两地间的距离为 如图,矩形ABCD被分割成六个正方形,其中最小正方形的面积等于4,则矩形ABCD的周长为
如图,矩形ABCD被分割成六个正方形,其中最小正方形的面积等于4,则矩形ABCD的周长为