题目内容
 如图,直线AB与x轴交于点A(2,0),与y轴交于B点,并且△AOB的面积为3.
如图,直线AB与x轴交于点A(2,0),与y轴交于B点,并且△AOB的面积为3.(1)求直线AB的函数关系式;
(2)若C是直线AB上的一点,且△BOC的面积是6,求点C的坐标.
考点:待定系数法求一次函数解析式,一次函数图象上点的坐标特征
专题:
分析:(1)结合图形,利用△AOB的面积为3和点A(2,0),求得点B的坐标为(0,3),设直线AB的函数关系式y=kx+b;
(2)分两种情况探讨:当点C在射线AB上时,当点C在射线BA上时,利用△BOC的面积是6,得出C点的横坐标为4或-4,代入求得纵坐标即可.
(2)分两种情况探讨:当点C在射线AB上时,当点C在射线BA上时,利用△BOC的面积是6,得出C点的横坐标为4或-4,代入求得纵坐标即可.
解答:解:(1)∵点A(2,0),△AOB的面积为3,
∴
×OA×OB=3
∴OB=3
∴点B的坐标为(0,3),
设直线AB的函数关系式y=kx+b,
代入点A、B坐标得,
,
解得k=-1.5,b=3
∴直线AB的函数关系式y=-1.5x+3;
(2)OB=3,△BOC的面积是6,
①当点C在射线AB上时,
得出C点的横坐标为-4,
∴y=-1.5x+3=9;
C点坐标为(-4,9);
②当点C在射线BA上时,
得出C点的横坐标为4,
∴y=-1.5x+3=-3;
C点坐标为(4,-3).
综上所知C点坐标为(-4,9)或(4,-3).
∴
| 1 |
| 2 |
∴OB=3
∴点B的坐标为(0,3),
设直线AB的函数关系式y=kx+b,
代入点A、B坐标得,
|
解得k=-1.5,b=3
∴直线AB的函数关系式y=-1.5x+3;
(2)OB=3,△BOC的面积是6,
①当点C在射线AB上时,
得出C点的横坐标为-4,
∴y=-1.5x+3=9;
C点坐标为(-4,9);
②当点C在射线BA上时,
得出C点的横坐标为4,
∴y=-1.5x+3=-3;
C点坐标为(4,-3).
综上所知C点坐标为(-4,9)或(4,-3).
点评:此题考查待定系数法求函数解析式以及三角形面积计算公式的运用,注意分类探讨答案.

练习册系列答案
相关题目
 如图是由四个正方体摆成的立体图形,那么从上面看到的平面图形是( )
如图是由四个正方体摆成的立体图形,那么从上面看到的平面图形是( )A、 |
B、 |
C、 |
D、 |
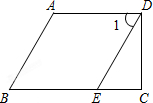 如图,AD∥BC,∠1=∠B.
如图,AD∥BC,∠1=∠B. 已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题:
已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题: 如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB、BC于点G、H.
如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB、BC于点G、H.