题目内容
13.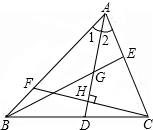 如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,其满足BE⊥AC;F为AB上一点,且CF⊥AD于H,下列判断:
如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,其满足BE⊥AC;F为AB上一点,且CF⊥AD于H,下列判断:①线段AG是△ABE的角平分线;
②BE是△ABD边AD上的中线;
③线段AE是△ABG的边BG上的高;
④∠1+∠FBC+∠FCB=90°.
其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据三角形的角平分线、三角形的中线、三角形的高的概念进行判断.
②根据三角形的中线定义判断.
③根据高线的定义进行判断.
④根据外角与内角的关系进行判断.
解答  解:①∵∠1=∠2,
解:①∵∠1=∠2,
∴AD平分∠BAC.
∴AG是△ABE的角平分线,
故①正确;
②∵G为AD中点,
∴AG=DG,
∴BG是△ABD边AD上的中线.
故②错误;
③∵BE⊥AC,
∴AE⊥BG,
∴线段AE是△ABG的边BG上的高.
故③正确;
④根据三角形外角的性质,∠1+∠AFH=∠1+∠FBC+∠FCB=90°,所以∠1+∠FBC+∠FCB=90°,
故④正确.
综上所述,正确的个数是3个.
故选:C
点评 本题考查了三角形的角平分线、三角形的中线、三角形的高的概念,注意:三角形的角平分线、中线、高都是线段,且都是顶点和三角形的某条边相交的交点之间的线段.透彻理解定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知Rt△ABC中,a、b为直角边,c为斜边,h为斜边上的高,则下面说法错误的是( )
| A. | ab=ch | |
| B. | h<a | |
| C. | 以ah、bh、ab为边的三角形是直角三角形 | |
| D. | 以a+b、ab、c为边的三角形是直角三角形 |
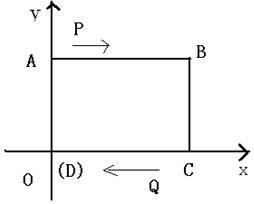 如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)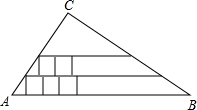 如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放22个.
如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放22个.