��Ŀ����
1��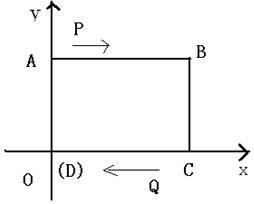 ��ͼ����֪��ƽ��ֱ������ϵ�У��ı���ABCD�dz����Σ���A=��B=��C=��D=90�㣬AB��CD��AB=CD=8cm��AD=BC=6cm��D����ԭ���غϣ�����Ϊ��0��0��
��ͼ����֪��ƽ��ֱ������ϵ�У��ı���ABCD�dz����Σ���A=��B=��C=��D=90�㣬AB��CD��AB=CD=8cm��AD=BC=6cm��D����ԭ���غϣ�����Ϊ��0��0����1��д����B�����ꣻ
��2������P�ӵ�A������ÿ��3����λ���ȵ��ٶ����յ�B�����˶�������Q�ӵ�C������ÿ��4����λ���ȵ��ٶ�������CD���������˶�����P��Q����ͬʱ���������˶�ʱ��Ϊt����tΪ��ֵʱ��PQ��BC��
��3����Q�����й����У���Q�˶���ʲôλ��ʱ��ʹ��ADQ�����Ϊ9�����ʱQ������꣮
���� ��1�����ݳ����ε�����ֱ�ӵó���B���ꣻ
��2�������˶��ص㣬��ƽ���ߵ����ʼ��ɵó�AP=OQ���������̼������ʱ��t��
��3�����������ε������ʽ���OQ���ɣ�
��� �⣺��1�����ı���ABCD�dz����Σ�AB=CD=8cm��AD=BC=6cm��
��B��8��6����
��2�����˶�֪��AP=3t��CQ=4t��
��OQ=AD-CQ=8-4t��
��PQ��BC��
��AP=OQ��
��3t=8-4t��
��t=$\frac{8}{7}$��
�൱tΪ$\frac{8}{7}$ʱ��PQ��BC��
��3��
�ߡ�ADQ�����Ϊ9��
��S��ADQ=$\frac{1}{2}$��OQ��AD=$\frac{1}{2}$��OQ��6=9��
��OQ=3��
��Q��3��0����-3��0��
������Q�˶�����ԭ��3cmλ��ʱ��ʹ��ADQ�����Ϊ9����ʱQ������꣨3��0����-3��0����
���� �������ı����ۺ��⣬��Ҫ�����˳��������ʣ�ƽ���ߵ����ʣ������ε������ʽ���Ȿ��Ĺؼ��Ǹ��������ʾ��AP��DQ����һ���Ƚϼ��п������⣮

��ϰ��ϵ�д�
�����Ŀ
3��
| ����ʽ | 0.2n | -$\frac{2{m}^{3}n{p}^{2}}{7}$ | $\frac{3}{5}$��r2 | -24x2y2 |
| ϵ�� | 0.2 | -$\frac{2}{7}$ | $\frac{3}{5}��$ | -24 |
| ���� | 1 | 6 | 2 | 4 |
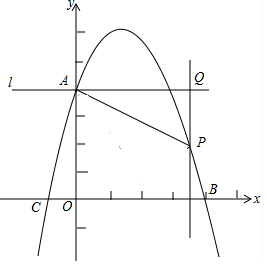 ��֪������y=-x2+3x+4��y���ڵ�A����x���ڵ�B��C����B�ڵ�C���Ҳࣩ������A����ֱ��y���ֱ��l����λ��ֱ��l�·�������������ȡһ��P������P��ֱ��PQƽ����y�ύֱ��l�ڵ�Q������AP��
��֪������y=-x2+3x+4��y���ڵ�A����x���ڵ�B��C����B�ڵ�C���Ҳࣩ������A����ֱ��y���ֱ��l����λ��ֱ��l�·�������������ȡһ��P������P��ֱ��PQƽ����y�ύֱ��l�ڵ�Q������AP��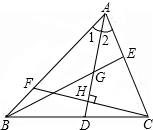 ��ͼ����ABC�У���1=��2��GΪAD�е㣬�ӳ�BG��AC��E��������BE��AC��FΪAB��һ�㣬��CF��AD��H�������жϣ�
��ͼ����ABC�У���1=��2��GΪAD�е㣬�ӳ�BG��AC��E��������BE��AC��FΪAB��һ�㣬��CF��AD��H�������жϣ�