题目内容
3.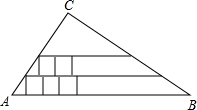 如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放22个.
如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放22个.
分析 求出AB的长后,根据相似的判定与性质每一层的靠上的边的长度,从而判定可放置的正方形的个数及层数.
解答 解:由勾股定理得:AB=$\sqrt{{5}^{2}+1{2}^{2}}$=13.
由三角形的面积计算公式可知:△ABC的高=$\frac{5×12}{13}$=$\frac{60}{13}$.
如图所示:根据题意有:△CAB∽△CEF
∴$\frac{EF}{AB}$=$\frac{\frac{60}{13}-1}{\frac{60}{13}}$=$\frac{47}{60}$
∴EF=$\frac{13×47}{60}$=10$\frac{11}{60}$
∴第一层可放置10个小正方形纸片.
同法可得总共能放4层,依次可放置10、7、4、1个小正方形纸片,
∴最多能叠放10+7+4+1=22(个)
故答案为:22个.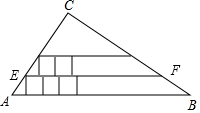
点评 本题考查了相似三角形的性质与判定、正方形的性质等问题,解题的关键是在掌握所需知识点的同时,要具有综合分析问题、解决问题的能力.

练习册系列答案
相关题目
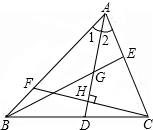 如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,其满足BE⊥AC;F为AB上一点,且CF⊥AD于H,下列判断:
如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,其满足BE⊥AC;F为AB上一点,且CF⊥AD于H,下列判断: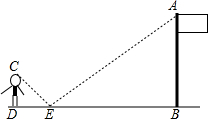 如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.
如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.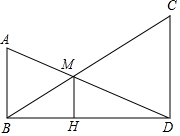 如图,AB和CD表示两根立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M.已知AB=10m,CD=15m,则点M离地面的高度MH=6m.
如图,AB和CD表示两根立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M.已知AB=10m,CD=15m,则点M离地面的高度MH=6m.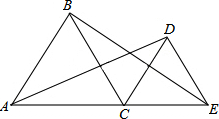 如图,已知C为线段AE上的一个动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,连接AD,BE,AC=5,AD=7,则BE=7.
如图,已知C为线段AE上的一个动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,连接AD,BE,AC=5,AD=7,则BE=7.