题目内容
6.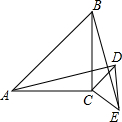 如图,△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE.
如图,△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE.(1)求证:AD=BE;
(2)当CD∥AB,AD=AB时,求证:∠CEB=2∠CBE;
(3)在(2)的条件下,已知AB=2,求CD的长.
分析 (1)欲证明AD=BE,只要证明△ACD≌△BCE即可.
(2)作DM⊥AB于M,CN⊥AB于N,先证明∠DAB=30°,再分别求出∠CBE,∠CEB的度数即可.
(3)根据CD=MN=AM-AN,分别求出AM、AN即可解决问题.
解答 (1)证明:∵AC=BC,CD=CE,∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴AD=BE.
(2)作DM⊥AB于M,CN⊥AB于N.
∵CA=CB,CN⊥AB,
∴AN=BN,∵∠ACB=90°,
∴CN=$\frac{1}{2}$AB,
∵CN∥DM,CD∥MN,
∴四边形MNCD是平行四边形,
∵∠DMN=90°,
∴四边形MNCD是矩形,
∴DM=CN=$\frac{1}{2}$AB=$\frac{1}{2}$AD,
∴∠DAM=30°,
∵CD∥AB,
∴∠ADC=∠DAB=30°,
∵∠CAB=45°,
∴∠CAD=15°,
∵△ACD≌△BCE,
∴∠CBE=∠CAD=15°,∠ADC=∠BEC=30°,
∴∠CEB=2∠CBE.
(3)由(2)可知四边形MNCD是矩形,
∴DM=CN=AN=BN=$\frac{1}{2}$AB=1,CD=MN,
在RT△ADM中,∵AD=2,DM=1,
∴AM=$\sqrt{A{D}^{2}-D{M}^{2}}$=$\sqrt{3}$,
∴CD=MN=AM-AN=$\sqrt{3}$-1.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理、直角三角形30°的判定等知识,解题的关键是灵活运用全等三角形的判定和性质、学会条件常用辅助线,属于中考常考题型.

| A. | x=1 | B. | x=-1 | C. | x=$\frac{3}{5}$ | D. | 无解 |
 根据有理数a,b在数轴上的位置(如图),则有下列六个不等式:①a-b>0;②a+b<0;③ab<0;④b2-a2>0;⑤$\frac{1}{a}$-$\frac{1}{b}$<0;⑥|a|-|b|>0,其中错误的是②③④⑥(只填序号).
根据有理数a,b在数轴上的位置(如图),则有下列六个不等式:①a-b>0;②a+b<0;③ab<0;④b2-a2>0;⑤$\frac{1}{a}$-$\frac{1}{b}$<0;⑥|a|-|b|>0,其中错误的是②③④⑥(只填序号).
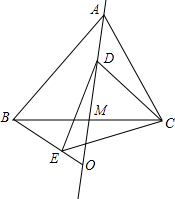 如图,在等边△ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.
如图,在等边△ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.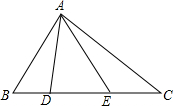 在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.
在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.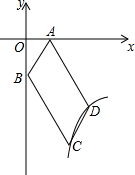 如图,四边形ABCD是?,AD=2CD,A(1,0),B(0,-2),双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,设D(a、b).
如图,四边形ABCD是?,AD=2CD,A(1,0),B(0,-2),双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,设D(a、b).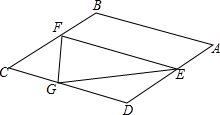 如图,在菱形ABCD中,AB=$\sqrt{3}$,∠B=120°,E是AD边上的一个动点(不与点A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.
如图,在菱形ABCD中,AB=$\sqrt{3}$,∠B=120°,E是AD边上的一个动点(不与点A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.