题目内容
15.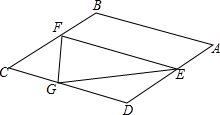 如图,在菱形ABCD中,AB=$\sqrt{3}$,∠B=120°,E是AD边上的一个动点(不与点A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.
如图,在菱形ABCD中,AB=$\sqrt{3}$,∠B=120°,E是AD边上的一个动点(不与点A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.(1)当△EFG为等腰三角形时,求DE的长;
(2)当△EFG为等腰三角形时,求△EFG与菱形ABCD的面积比.
分析 (1)由四边形ABCD是菱形,得到BC∥AD,由于EF∥AB,得到四边形ABFE是平行四边形,根据平行四边形的性质得到EF∥AB,于是得到EF=AB=$\sqrt{3}$,当△EFG为等腰三角形时,①EF=GE=$\sqrt{3}$时,于是得到DE=DG=$\frac{1}{2}$AD=$\frac{\sqrt{3}}{2}$,②GE=GF时,根据勾股定理得到DE=$\frac{\sqrt{3}}{3}$;
(2)当△EFG为等腰三角形时,EG2+FG2=EF2时根据三角函数的定义得到GE=$\frac{3}{2}$,GF=$\frac{\sqrt{3}}{2}$,根据三角形和菱形的面积公式即可得到结论.
解答 解:(1)∵四边形ABCD是菱形,
∴BC∥AD,
∵EF∥AB,
∴四边形ABFE是平行四边形,
∴EF∥AB,
∴EF=AB=$\sqrt{3}$,
当△EFG为等腰三角形时,
①EF=GE=$\sqrt{3}$时,则DE=DG=$\frac{1}{2}$AD=$\frac{\sqrt{3}}{2}$,
②GE=GF时,($\sqrt{3}DE)$2=($\frac{\sqrt{3}}{2}$DE)2+($\sqrt{3}$-DE-$\frac{1}{2}$DE)2,解得DE=$\frac{\sqrt{3}}{3}$;
(2)当△EFG为等腰三角形时,EG2+FG2=EF2时,
∵GD=DE,
∴∠DGE=∠DEG=30°,
∴∠FEG=30°,
∴$\frac{GE}{EF}$=sin60°,
∴$\frac{GE}{\sqrt{3}}=\frac{\sqrt{3}}{2}$,
∴GE=$\frac{3}{2}$,
∴GF=$\frac{\sqrt{3}}{2}$,
∴$\frac{{S}_{△EFG}}{{S}_{菱形ABCD}}$=$\frac{\frac{1}{2}×\frac{\sqrt{3}}{2}×\frac{3}{2}}{\frac{1}{2}×3×\sqrt{3}}$=$\frac{1}{4}$.
点评 本题考查了菱形的性质,平行四边形的性质,等腰三角形的性质,熟练则菱形的性质是解题的关键.

 △ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
△ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
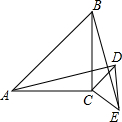 如图,△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE.
如图,△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE.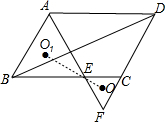 如图,在?ABCD中,∠A的平分线分别与BC及DC的延长线交于点E、F,点O、O1分别为△CEF、△ABE的外心
如图,在?ABCD中,∠A的平分线分别与BC及DC的延长线交于点E、F,点O、O1分别为△CEF、△ABE的外心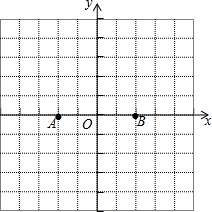 如图,在平面直角坐标系中,已知点A(-2,0),B(2,0).
如图,在平面直角坐标系中,已知点A(-2,0),B(2,0). 如图,在?ABCD中,有下列四个条件:①AC=AD;②BA=BC;③∠ABC=90°;④AC=BD.添加其中的一个条件后,还不能使?ABCD成为菱形,则所添加的条件是①③④.
如图,在?ABCD中,有下列四个条件:①AC=AD;②BA=BC;③∠ABC=90°;④AC=BD.添加其中的一个条件后,还不能使?ABCD成为菱形,则所添加的条件是①③④.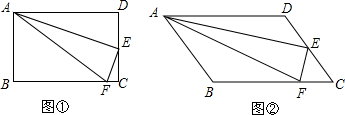
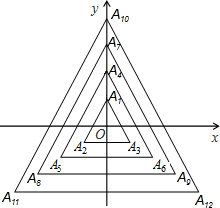 如图,所有的三角形都有一个顶点位于y轴上,另外两个顶点分别位于三、四象限,且位于y轴上的点到原点的距离,与位于三、四象限内的点到两坐标轴的距离都相等,这些距离从内到外分别是1、2、3…,顶点依次用A1、A2、A3、A4…表示,则顶点A2011的坐标是(0,670).
如图,所有的三角形都有一个顶点位于y轴上,另外两个顶点分别位于三、四象限,且位于y轴上的点到原点的距离,与位于三、四象限内的点到两坐标轴的距离都相等,这些距离从内到外分别是1、2、3…,顶点依次用A1、A2、A3、A4…表示,则顶点A2011的坐标是(0,670).