题目内容
14.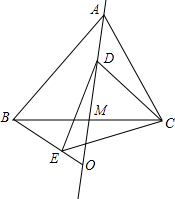 如图,在等边△ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.
如图,在等边△ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.(1)如图1,点D在线段AM上,①求证:AD=BE;②求证:∠AOB=60°
(2)当动点D在线段MA的延长线上时,试判断(1)中∠AOB的度数是否会发生改变?并说明理由.
分析 (1)①如图1中,只要证明△ACD≌△BCE即可.
②先证明∠CAM=30°,由△ACD≌△BCE得∠OBM=∠CAM=30°,由此即可解决问题.
(2)如图②中,结论不变.证明方法类似(1).
解答 (1)证明:①如图1中,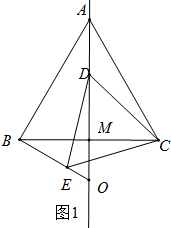 ∵△ABC和△DCE都是等边三角形,
∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴AD=BE
②∵BM=CM,AB=AC,∠BAC=60°,
∴AM⊥BC,∠BAM=∠CAM=30°,
∴∠AMC=∠MBO=90°,
∵△ACD≌△BCE,
∴∠OBM=∠CAM=30°,
∵∠OBM+∠BOM=90°
∴∠AOB=60°
(2)如图②中,结论:∠AOB的度数不变.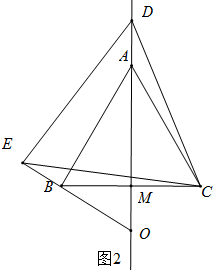 理由:∵△ABC和△DCE都是等边三角形,
理由:∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
:∵BM=CM,AB=AC,∠BAC=60°,
∴AM⊥BC,∠BAM=∠CAM=30°,
∴∠AMC=∠MBO=90°,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠DAC=∠EBC,
∴∠OBM=∠CAM=30°,
∴∠AOB=90°-∠OBM=60°.
点评 本题考查全等三角形的判定和性质、等边三角形的判定和性质,解题的关键是正确寻找全等三角形,灵活运用全等三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
5.若圆锥的底面半径为3cm,展开后所得扇形的半径为4cm,则它的侧面积等于( )
| A. | 12πcm2 | B. | 6πcm2 | C. | 12cm2 | D. | 24πcm |
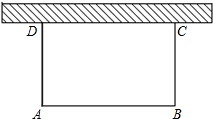 如图,用长为30米的篱笆围成一个一边靠墙的矩形养鸡场ABCD,已知墙长14m,设边AD的长为x(m),矩形ABCD的面积为y(m2).
如图,用长为30米的篱笆围成一个一边靠墙的矩形养鸡场ABCD,已知墙长14m,设边AD的长为x(m),矩形ABCD的面积为y(m2).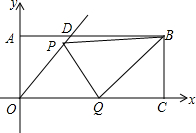 在平面直角坐标系x、y中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P在线段OD上,点Q线段OC上,OQ=$\sqrt{2}$OP,∠PQB=90°,求线段PO的长.
在平面直角坐标系x、y中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P在线段OD上,点Q线段OC上,OQ=$\sqrt{2}$OP,∠PQB=90°,求线段PO的长.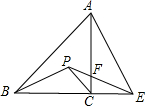 如图,在等腰Rt△ABC中,AC=BC,E为BC的延长线上一点,连接AE,若线段AE的中垂线交∠ABC的平分线于点P,交AC于点F.
如图,在等腰Rt△ABC中,AC=BC,E为BC的延长线上一点,连接AE,若线段AE的中垂线交∠ABC的平分线于点P,交AC于点F.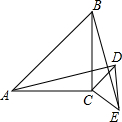 如图,△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE.
如图,△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE.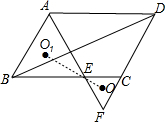 如图,在?ABCD中,∠A的平分线分别与BC及DC的延长线交于点E、F,点O、O1分别为△CEF、△ABE的外心
如图,在?ABCD中,∠A的平分线分别与BC及DC的延长线交于点E、F,点O、O1分别为△CEF、△ABE的外心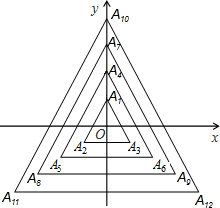 如图,所有的三角形都有一个顶点位于y轴上,另外两个顶点分别位于三、四象限,且位于y轴上的点到原点的距离,与位于三、四象限内的点到两坐标轴的距离都相等,这些距离从内到外分别是1、2、3…,顶点依次用A1、A2、A3、A4…表示,则顶点A2011的坐标是(0,670).
如图,所有的三角形都有一个顶点位于y轴上,另外两个顶点分别位于三、四象限,且位于y轴上的点到原点的距离,与位于三、四象限内的点到两坐标轴的距离都相等,这些距离从内到外分别是1、2、3…,顶点依次用A1、A2、A3、A4…表示,则顶点A2011的坐标是(0,670).